Le sol, un réservoir d’eau très particulier

Selon la quantité d’eau présente dans le sol, celle-ci est plus ou moins fortement liée au substrat. On distingue couramment quatre catégories d’eau qui correspondent à différents degrés de liaison entre les molécules d’eau et le sol. La notion de degré de liaison introduite ici de façon qualitative, peut se comprendre comme la quantité d’énergie nécessaire pour extraire l’eau liée et l’amener à l’état libre, ce qui correspond en fait à la définition qui sera donnée plus loin du potentiel hydrique (§ III.2.2). Noter que le potentiel hydrique est aussi abondamment utilisé pour caractériser l’état de l’eau dans la plante et dans l’atmosphère.

Ainsi distingue-t-on habituellement :

-  l’eau gravitaire qui circule librement dans l’espace poral, notamment sous l’effet de la gravité (percolation). L’énergie de liaison de l’eau au substrat est donc très faible ;

-  l’eau capillaire, faiblement liée au substrat par les forces de capillarité ou de tension superficielle qui se manifestent lorsque des ménisques air-eau se sont formés. Cette catégorie représente ordinairement la majeure partie de l’eau accessible aux racines des plantes ;

-  l’eau adhérente aux particules solides, assez fortement liée au substrat par des forces électriques, sous forme de films ; cette dernière est d’ailleurs la seule qui reste retenue par le sol lorsqu’il se trouve en équilibre avec la vapeur d’eau atmosphérique ;

-  l’eau de constitution, constitutive des minéraux et argiles du sol, totalement inaccessible pour les plantes. Lorsqu’on dessèche un échantillon de sol par étuvage à 105°C pendant 24h (protocole standard pour la mesure de l’humidité pondérale) seule subsiste conventionnellement l’eau de constitution.

Ces deux dernières fractions sont totalement inaccessibles aux plantes. L’eau adhérente aux particules solides et l’eau dite de constitution concerne de l’eau fortement liée aux cations hydratés retenus par des liaisons électrostatiques à la surface chargée négativement des argiles et des matières organiques.

D’un point de vue macroscopique l’état de l’eau contenue dans un sol peut se caractériser de deux façons :

       - quantitativement sur une base massique ou volumique : l’humidité pondérale (H_p) et l’humidité volumique (H_v), grandeurs extensives,

       - énergétiquement, par la notion de potentiel hydrique (Y), grandeur intensive.

La quantité d’eau que les plantes peuvent extraire du sol dépend de ces deux types de grandeurs. Nous les présenterons d’abord séparément. Puis nous étudierons la relation qui existe entre elles, relation très importante pour caractériser un sol en tant que réservoir d’eau pour les plantes. On retrouvera une présentation analogue dans le Chap. II.3 consacré à la caractérisation de l’état hydrique d’un échantillon végétal.

 

III.1. Grandeurs massiques et volumiques caractérisant l’eau d’un sol 

 

III.1.1. L’humidité pondérale H_p, ou teneur massique en eau

C’est le rapport de la masse d’eau sur celle de la phase solide :

                                                                        équation 6

avec :

M_eau= masse d’eau de l’échantillon obtenue par différence entre la masse du sol frais et celle du sol sec
M_{sol sec}= masse de l’échantillon de sol sec, passé à l’étuve à 105°C jusqu’à l’obtention d’un poids constant
H_p est un nombre sans dimension qui s’exprime souvent en pourcents : H_p= 0,15 (ou 15%). H_p varie généralement, pour des sols minéraux, de 5 à 40%. Dans le cas de sols organiques (tourbe) H_p peut largement dépasser les 100% et atteindre 1000%, voire plus.

 

III.1.2. L’humidité volumique H_v ou teneur volumique en eau

C’est le rapport du volume de l’eau à celui de l’échantillon de sol en place :

                                                                                                équation 7

avec :

V_eau = volume d’eau contenu dans l’échantillon, obtenu par différence entre le poids frais du sol en place et son poids sec
V_Sap = volume de l’échantillon en place, appelé aussi volume apparent.
H_v est un nombre sans dimension ; des valeurs moyennes de H_v sont de 7 à 15 % pour un sol sableux, de 20 à 45% pour un sol limoneux et de 30 à 60 % pour un sol très argileux. Les humidités volumique et pondérale sont liées par la relation :

                                                                                                    équation 7bis

avec d_ap  = densité apparente (Cf. équation 1bis)

Très généralement, sauf dans des substrats tourbeux ou dans les premiers cm en surface de sols classiques, la densité apparente d’un sol d_ap est supérieure à 1, ce qui entraine que la valeur numérique de H_v est telle que H_v > H_p.

Pour un échantillon donné de sol, l’humidité pondérale a une valeur bien définie, indépendante de la structure contrairement à l’humidité volumique qui en dépend : si le volume du sol diminue, par tassement par exemple, H_v va augmenter.

La connaissance de l’humidité volumique H_v est souvent recherchée en agronomie notamment pour réaliser le bilan hydrique à l’échelle de la parcelle. En effet, si l’on considère une tranche de sol d’épaisseur Dz donnée et d’humidité volumique H_v, le produit H_v.Dz représente l’épaisseur d’eau présente dans cette tranche, exprimée par exemple en mm d’eau. On pourra ainsi calculer le stock d’eau accessible aux plantes si l’on connaît le profil d’humidité volumique dans la zone racinaire, en faisant la somme sur tout le profil des épaisseurs d’eau élémentaires :

                                                                         équation 8

Cette grandeur est directement comparable aux autres grandeurs déterminantes du bilan hydrique (voir en particulier les Chap. IV.1 et IV.3) comme la pluviométrie, l’évapotranspiration ou le drainage, qui toutes s’expriment aussi en mm d’eau.

Par ailleurs, l’humidité volumique H_v peut être directement comparée à la porosité totale P_t. En effet, quand le sol est à saturation, le volume occupé par l’eau est proche de l’espace poral total P_t car très peu d’air reste emprisonné. L’humidité volumique maximale est donc égale à la porosité totale (équation 3). Ainsi connaissant d’un côté cette porosité totale, de l’autre l’humidité volumique, on peut se faire une idée assez précise du volume de la phase gazeuse correspondant à cette humidité et par là, des conditions d’aération des racines : plus leur rapport est voisin de 1, plus mauvaise est l’aération.

Pour les méthodes de mesure de l’humidité, de la porosité et de la densité on se reportera aux ouvrages spécialisés (Musy et Soutter, 1991, Calvet 2003)

On verra ci-dessous (III.3 et II.4) que deux valeurs de l’humidité d’un sol, la capacité au champ et le point de flétrissement permanent sont particulièrement importantes pour caractériser un sol en tant que réservoir d’eau pour les plantes.

 

III.2 Grandeur énergétique caractérisant l’eau du sol : le potentiel hydrique Y_s et ses composantes

Examinons tout d’abord d’un point de vue phénoménologique ce qui se passe lorsque le sol se dessèche, que ce soit sous l’effet de l’évaporation ou de l’extraction d’eau par les racines des plantes.

III.2.1. Drainage progressif d’un échantillon de sol par succion.

Un procédé pour contrôler le degré de liaison de l’eau dans un échantillon de sol consiste à utiliser la technique de la plaque de succion (Fig. 7a). L’échantillon de sol saturé est placé sur une plaque de porcelaine poreuse elle-même saturée d’eau et reliée à un réservoir dont nous allons faire varier le niveau z par rapport au plan de référence z. Conformément aux lois de l’hydrostatique, l’équilibre dans un tel dispositif (absence de mouvement d’eau) suppose que la pression de l’eau dans un plan horizontal soit uniforme. La pression atmosphérique P_atm s’exerce en permanence sur l’eau du réservoir au niveau z.

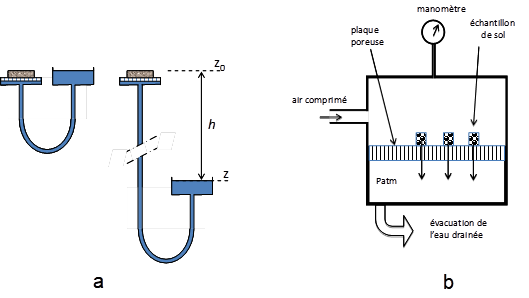
Figure 7. a : Expérience de drainage progressif sur une table de succion ; b : schéma de l’appareil de Richards

Etat initial : saturation (Fig. 7a gauche : z=z)

La surface de l’eau du réservoir et l’échantillon de sol sont au même niveau z (niveau de référence). D’un point de vue physique, toute la porosité du sol est occupée par de l’eau. La pression dans l’eau est égale à la pression dans l’air, soit la pression atmosphérique P_atm, de sorte que la surface de séparation air/eau (interface) est plane aussi bien dans le réservoir que pour l’échantillon de sol. Dans la suite, cet état nous servira de référence et correspondra par définition au potentiel hydrique nul : Y_s=0.

Expérience de drainage progressif 

Abaissons le réservoir d’eau d’une hauteur h n’excédant pas quelques centimètres (Fig. 7a, droite). A l’équilibre, au niveau z la pression est toujours égale à P_atm , mais dans le sol, la pression P_eaudans l’eau au niveau z devient :

P_eau = P_atm – hrg

r : masse volumique de l’eau (1000 kg m^-3)
g : accélération de la pesanteur (9,81 m s^-2)

La valeur de P_eau est alors inférieure à la pression atmosphérique ; l’eau du sol est en dépression (pression relative négative ou succion). L’existence d’une différence de pression entre l’air et l’eau du sol implique une courbure des interfaces air/eau conformément à la loi de Laplace – Young (simplifiée ici en supposant une interface sphérique et un angle de mouillage nul ; voir Chap. I.3) :

                                                                   équation 9

avec :

R_c = rayon de courbure de l’interface (supposée sphérique)
g : tension superficielle de l’eau (73.10^-3 N.m^-1 à 20°C)

Ecrite autrement l’équation 9 permet d’exprimer le rayon de courbure des ménisques air/eau en fonction de h :

                                                                                          équation 9bis

R_c varie comme l’inverse de la hauteur h et tend vers zéro pour des dénivellations h (des succions) de plus en plus grandes.

Si tous les pores du sol sont d’un rayon supérieur à Rc, il ne se passe rien d’autre qu’une modification de l’aspect de la surface du sol qui cesse d’être saturée. Du point de vue des propriétés hydrodynamiques du sol nous sommes toujours dans le domaine saturé : teneur en eau et conductivité hydraulique sont maximales. Dans un sol en place cela correspond à la frange capillaire, c’est à dire une zone de sol saturée qui se développe sur quelques centimètres au-dessus d’une nappe phréatique.

Continuons à baisser le réservoir. Pour une certaine hauteur h_ea le rayon de courbure Rc des ménisques devient inférieur au rayon des pores les plus gros R_max. A ce stade, ces pores se vident de leur eau et une petite quantité d’air commence à entrer dans l’échantillon de sol. On a atteint ce que l’on appelle la pression d’entrée d’air P_ea, dont on voit qu’elle dépend principalement de la macroporosité :

                                                                                                                                                      équation 10       

On entre alors dans le domaine non saturé qui implique une réduction de la conductivité hydraulique.

Poursuivons l’expérience. Au fur et à mesure que l’on abaisse le réservoir on draine des pores de rayons de plus en plus petits et l’échantillon de sol devient de plus en plus sec.

Cette configuration expérimentale ne permet cependant pas d’atteindre des niveaux de dessèchement comparables à ceux atteints dans la nature sous l’effet de l’extraction racinaire. D’une part le procédé est très peu pratique, d’autre part deux phénomènes physiques imposent une limite à la poursuite de l’expérience :

1-      Lorsque la hauteur h atteint 6 à 7 mètres, la pression au niveau de référence z devient très faible (de l’ordre de 30 kPa) et l’eau a tendance à passer à l’état vapeur (phénomène de cavitation), de sorte que le dispositif se désamorce.

2-      L’entrée d’air dans la plaque de porcelaine poreuse qui cesse d’être saturée, ce qui a finalement le même effet.

On peut néanmoins réaliser une expérience équivalente à ce que nous venons de décrire (drainage par dépression) mais de façon beaucoup plus pratique, dans l’appareil de Richards (Fig. 7b). Dans cette configuration, c’est la pression dans l’air qui est augmentée à volonté alors que la pression dans l’eau du sol et sous la plaque poreuse reste égale à la pression atmosphérique. Il n’y a donc plus de risque de cavitation. On obtient à l’équilibre une répartition de l’eau identique à celle que l’on aurait eue avec la technique par succion puisqu’en définitive c’est la géométrie des pores et la différence de pression air-eau qui détermine quels pores sont drainés. Dans les deux cas, le rayon maximal des pores qui restent pleins d’eau est donné par :

                                                                                         équation 11

Par exemple, si la surpression d’air imposée dans l’appareil de Richards est égale à 1 bar (100 kPa), le rayon maximum des pores qui restent remplis d’eau est de l’ordre de 1,5 mm. Cet appareil permet entre autre d’établir la relation dite potentiel  humidité dont nous reparlerons plus loin (§ III.3).

La figure 8 montre schématiquement comment se modifie la répartition de l’eau entre les particules solides de sol en fonction de l’écart de pression entre l’air et l’eau.

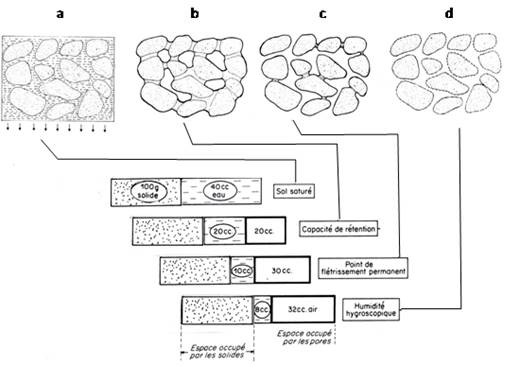
Figure 8. Schéma de la  répartition de l’eau dans l’espace poral d’un sol, pour différentes humidités. a) Sol saturé : l’eau s’écoule par gravité. Tout l’espace poreux est occupé par l’eau. b) Sol à la capacité au champ. L’eau occupe encore une grande partie de l’espace poreux mais de l’air est présent. c) Sol au point de flétrissement permanent. La fraction de l’espace poreux occupée par l’eau a diminué : elle est restreinte à des ménisques air-eau capables de soutenir des tensions de l’ordre de -1,5 à -2,0 MPa. d) Sol très sec. L’eau qui demeure est dite eau hygroscopique, en équilibre  avec l’humidité atmosphérique. Les rectangles donnent des ordres de grandeurs des volumes relatifs des phases solide, liquide et gazeuse aux différentes humidités. D’après Callot et al. (1982).

Comme nous le verrons plus loin le raisonnement précédent sur la taille des pores peut être concomitant avec un changement de géométrie du sol (gonflement lors de l’humectation, retrait lors de la dessiccation).

 

III.2.2. Le potentiel hydrique

Comme signalé au début de ce paragraphe, outre la quantité d’eau présente dans un sol, il importe de caractériser l’état énergétique de cette eau, c'est-à-dire son potentiel hydrique (voir Chap. I.2). La notion de potentiel hydrique Y, utilisée en sciences de l’environnement, biologie etc., n’est autre que le potentiel chimique de l’eau. De façon un peu simplifiée on peut le définir comme une mesure de la quantité d’énergie qu’il faudrait fournir à un kg d’eau liée pour l’amener à l’état d’eau libre. Y s’exprime donc selon cette définition en J kg^-1. Mais il est très souvent exprimé en unités de pression (Pascal, bar …) ce qui correspond à des Joules par unité de volume (1 Pa = 1 J m^-2). La connaissance de cette grandeur est indispensable pour déterminer si l’eau présente dans un sol est ou non utilisable par les plantes. Ce sont en effet les différences de potentiel hydrique entre deux points et non les différences d’humidité qui sont responsables des flux d’eau qui peuvent circuler dans le sol et entre le sol et la plante.

Comme pour les plantes, il est important de considérer les principales composantes du potentiel hydrique dans le sol. Elles sont au nombre de quatre[1], chacune traduisant l’effet d’un phénomène particulier sur l’état énergétique de l’eau. Le potentiel hydrique total Y_T  est donné par la somme de ces composantes (Cf. Chap. I.2 équation 20) :

Y_T  = Y_m + Y_g + Y_p + Y_p                                                        équation 12

avec :

Y_m  : potentiel matriciel qui représente l’effet des forces capillaires et d’adsorption. Le qualificatif matriciel exprime que cette composante résulte des propriétés de la « matrice-sol ». Elle concerne exclusivement le domaine non saturé et traduit l’effet des forces capillaires (interfaces air-eau) et d’adsorption qui tendent à maintenir l’eau dans les pores du sol et à la surface des particules. C’est la composante principale du potentiel hydrique du sol dans le domaine non saturé ;

Y_g   = (z-z)rg       est le potentiel gravitationnel, proportionnel à l’accélération de la pesanteur ;

Y_p   = P est le potentiel hydrostatique ou de pression sous l’effet de la pression hydrostatique. Cette composante n’est à prendre en considération que pour les valeurs positives du potentiel, car pour les valeurs négatives elle se confond avec la composante matricielle. On ne la rencontrera donc que dans la nappe phréatique.

Y_p   = - p est le potentiel osmotique sous l’effet de la présence de solutés. Cette composante rend compte de la pression osmotique p de la solution du sol.

Rappelons que, par convention, la pression osmotique est positive mais que Y_p est < 0 (Cf. Chap. I.2). En général la concentration de la solution du sol en éléments dissous est faible (10^-4  ou 10^-3 molaire soit p = 0,2 à 2 kPa). Dans les sols salins toutefois, on peut rencontrer des concentrations bien supérieures, de l’ordre de 10^-2 à  10^-1 molaire, soit p = 20 à 200 kPa (= 0,2 à 2 bar). Par ailleurs la composante Y_p ne se manifeste concrètement qu’en présence d’une membrane semi-perméable. Le potentiel osmotique est donc le plus souvent négligé dans les sols agronomiques des régions tempérées alors qu’il ne peut l’être dans les régions à forte demande évaporatoire et sur des sols irrigués, ou encore contaminés par le milieu marin avec des eaux plus ou moins chargées en sels, notamment NaCl.

Remarques :

a) Rappelons que le potentiel hydrique total Y_T correspond toujours à une différence (et non pas à une valeur absolue) entre l’état énergétique actuel de l’eau du sol (exprimé par unité de volume d’eau) et l’état énergétique du même volume d’eau dans l’état standard de référence. Cet état standard est celui d’un volume d’eau pour lequel toutes les composantes précédentes du potentiel hydrique sont simultanément nulles. Il s’agit donc d’eau pure (Y_p = 0) à l’altitude z, présentant une surface libre (pas de phénomènes capillaires ni de surface, Y_m = 0) à la pression atmosphérique normale.

b) La distinction formelle entre composante hydrostatique Y_p et composante matricielle Y_m est quelque peu arbitraire, car il n’y a pas de véritable discontinuité entre domaine saturé et non saturé. Il s’agit bien dans les deux cas de la « pression relative » de l’eau du sol, mais celle-ci est négative dans un sol non saturé par suite des  phénomènes d’adsorption et de capillarité alors qu’elle est positive ou nulle dans les sols saturés.

c) Dans un sol non saturé, les composantes de gravité (Y_g) et hydrostatique (Y_p) sont le plus souvent négligées dans l’expression du potentiel hydrique, la composante matricielle Y_m étant généralement de loin la plus importante.

d) Dans un sol saturé, le potentiel hydrique est déterminé par les seules composantes Y_g et Y_p. Pour les hydrauliciens du sol, la somme Y_g + Y_p est souvent exprimée en hauteur d’eau (m) et correspond à la notion de « charge hydraulique, H ».

 

Notion de pF 

Le pF est un autre mode d’expression du potentiel hydrique du sol, maintenant assez peu utilisé, même en science du sol et en horticulture (voir complément C1).. Pendant longtemps on a utilisé des hauteurs pour exprimer des pressions : cm d’eau ou mm de mercure. Ainsi par exemple une colonne d’eau de 10 m de haut exerce sur sa base une pression de 9,81 10⁴ Pa (98,1 kPa) soit environ 1 bar. Ainsi exprimé, le potentiel hydrique du sol se chiffre souvent en milliers ou dizaines de milliers de cm d’eau. De plus, la gamme des Y_m du sol est très étendue. Pour cette raison, Schofield (1935) a proposé une notation logarithmique, le « pF », par analogie avec le pH des chimistes. Le pF est le logarithme décimal de la valeur absolue du Y_m exprimée en cm d’eau :

                                                                                             équation 13

Citons deux valeurs particulières du pF qui ont été longtemps associées à deux valeurs caractéristiques de l’humidité des sols mesurées au laboratoire, très utiles en agronomie (voir § II.3.3) :

pF  = 2,5 à 2,7  (Y_m  = - 0,03 à - 0,05 MPa) correspond sensiblement à la capacité au champ ;

pF = 4,2          (Y_m = -1,56 MPa) fournit une bonne approximation du point de flétrissement permanent.

Dans la réalité ces « bornes » ne sont que des repères, qui varient sensiblement d’un type de sol à l’autre comme l’indique le Tableau 4 pour la capacité au champ, d’où la nécessité de réaliser des analyses de sol, notamment pour la gestion de l’irrigation.

 

Classes texturales	origine	humidité HCC (en % volumique)	Ycc (kPa)	pF
plus de 40% d’argile	colluviaux argileux	46	- 250	3.4
20% d’argile	terres franches d’alluvions	33	-100	3.0
moins de 10% d’argile avec sable fin	sables fauves	24	- 10	2.0
moins de 5% d’argile avec sable grossier		16	- 2	1.3

 

Tableau 4. Valeurs de l’humidité à la capacité au champ, H_CC, du potentiel hydrique Y_cc et du pF correspondants pour quelques types de sols. D’après Marty, 1969. On voit que le potentiel hydrique de la capacité au champ varie selon la texture du sol. On ne peut cependant lui faire correspondre une valeur unique car l’eau retenue dans le sol à la capacité au champ dépend de la hauteur de la colonne capillaire, elle-même en relation avec la profondeur du sol où des pores exploités par la faune et la rhizosphère sont présents.