Description détaillée du modèle
Demande transpiratoire et transpiration maximale
On calcule d’abord l’évapotranspiration potentielle encore appelée « demande climatique » (ETP, voir chapitres II.5, II.6 et IV.3) qui correspond à la demande transpiratoire imposée aux feuilles de la couronne de l’arbre par le climat. Une relation empirique permet alors de calculer la transpiration maximale de l’arbre TM soumis à ce niveau d’ETP. Cette relation a été obtenue sur une large gamme d’espèces, aussi bien feuillues que résineuses, dans différentes régions du monde (voir Granier et al., 1999). La transpiration maximale est atteinte lorsqu’il n’y a pas de limitations climatiques ni édaphiques et que les arbres ont atteint leur plein développement foliaire. Pour les arbres, TM est environ égal à 75% de ETP.
ETP est calculée avec la formule de Penman, qui est très largement utilisée en agronomie pour le calcul de l’irrigation des cultures. Le lecteur peut se reporter au chapitre II.5 qui détaille cette formule. La formule de Penman, qui peut paraître un peu compliquée, rassemble en fait deux composantes de la demande climatique : un terme « radiatif », qui dépend du rayonnement net reçu par la surface végétale et un terme « convectif » appelé pouvoir évaporant de l’air, qui dépend de l’humidité de l’air et du vent.
L’expression exacte de cette formule est donnée en Annexe 2.
Calcul de l’offre en eau au niveau du sol
Parallèlement, on calcule la fraction des précipitations qui alimente le sol. On sait que les arbres interceptent une part significative des précipitations (de 10 à 40%), qui retourne vers l’atmosphère (voir chapitre IV.3). Une petite pluie est totalement interceptée par le feuillage des arbres. Pour des pluies de plus en plus importantes, la proportion d’eau interceptée (In) diminue, devenant très faible pour les fortes pluies.
Lorsqu’il y a des précipitations, le taux d’interception est calculé par le modèle, dépendant principalement de l’intensité de la pluie, de l’ETP pendant celle-ci et de la surface foliaire de l’arbre. La relation entre l’interception et la pluie incidente est donnée par l’équation 1 et est représentée sur la figure 3 (voir Granier et al., 1999).
On voit que In est égal à 100% pour les pluies faibles, jusqu’à un certain seuil (P sur la figure 3), au-delà duquel In diminue. La forme de la diminution de In lorsque la pluie augmente est de type hyperbolique décroissant :
(équation 1)
où a, b et c sont les paramètres de l’équation, obtenus de façon expérimentale.
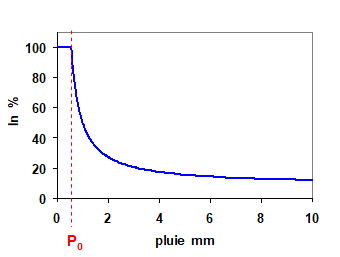
Figure 3. Relation entre l’interception (In) et la pluie incidente, en pourcentage de la pluie incidente.
Par différence entre la pluie et son interception, on calcule la pluie arrivant au sol.
On retranche la transpiration de l’arbre de l’heure précédente (ou de la demi-heure précédente, selon le pas de temps choisi). S’il y a excès d’eau, c'est-à-dire que la réserve utile est dépassée, cette eau est drainée. Au final on a ainsi calculé la réserve en eau du sol et sa fraction disponible pour l’arbre[1] . Une variable très intéressante pour les modèles est la réserve en eau relative dans le sol, que l’on écrit souvent REW (pour « relative extractable water »), qui représente la fraction de la réserve en eau utilisable par la plante à un moment donné. REW est calculé simplement comme égal au rapport R/RU, où R représente la réserve en eau extractible par la plante et RU la réserve utile du sol. Lorsque le sol est à la capacité au champ[2], REW=1 et lorsque le sol est totalement desséché par la plante, on a REW=0.
On calcule le potentiel hydrique du sol (Ys), qui est fonction de sa réserve en eau. Pour de fortes teneurs en eau, Ys proche de zéro.
Il faut que l’humidité du sol diminue fortement pour que le Ys commence à diminuer. Cette relation est représentée sur la figure 4 sur toute l’étendue de la réserve en eau du sol. Ce type de fonction utilisé couramment en écophysiologie et en physique du sol est présenté en annexe A3 en fin de ce chapitre.
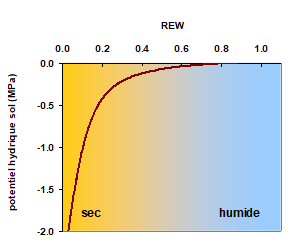
Figure 4. Relation entre le potentiel hydrique du sol et la réserve en eau disponible pour la plante (REW). Quand REW = 1, le sol est à son maximum d’hydratation. Quand REW = 0, il n’y a plus d’eau disponible pour les racines dans le sol. On dit que le sol a atteint le point de flétrissement permanent.
Transpiration réelle et conductivité hydraulique de l’arbre
En l’absence de contrainte hydrique imposée par le sol, la transpiration de l’arbre est égale à sa transpiration maximale TM. Lorsque la quantité d’eau disponible au niveau du sol descend au-dessous d’un seuil égal à 40% de la réserve utile (soit REW=0,4), elle devient limitante pour la plante, qui est alors soumise à une contrainte hydrique. La quantité d’eau disponible en-deçà de ce seuil est appelée réserve difficilement utilisable (RDU). Dans ces conditions limitantes, le potentiel thermodynamique de l’eau dans la plante (voir Chapitre I.2) s’abaisse et la plante régule ses échanges gazeux avec l’atmosphère au niveau des feuilles dont les stomates se ferment partiellement, ce qui réduit la transpiration maximale à un niveau inférieur : la transpiration réelle (T).
La figure 5 représente cette régulation : on y a reporté la relation entre la transpiration relative (=T/TM) en fonction de la réserve hydrique relative en eau dans le sol. On y voit que T/TM reste proche ou égal à 1 quand REW est supérieur ou égal à 0,4 et que ce rapport diminue fortement lorsque REW descend au-dessous de 0,4.
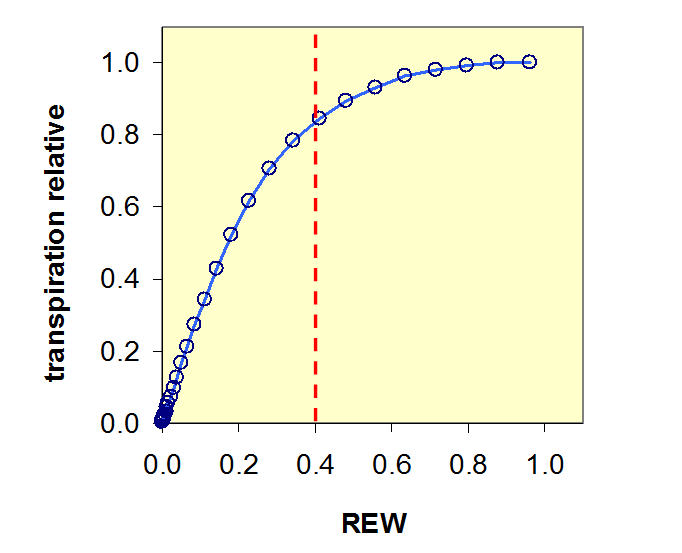
Figure 5. Relation entre la transpiration relative à son maximum possible et la réserve en relative dans le sol (REW). Le trait rouge en pointillé correspond au seuil de REW = 0,4 au-dessous duquel les stomates commencent à se fermer plus rapidement, réduisant la transpiration.
Parallèlement à la régulation stomatique, lorsqu’il y a une contrainte hydrique et que la plante transpire encore, la diminution du potentiel hydrique du sol provoque l’augmentation des tensions dans toute la plante, des racines aux feuilles. La conductivité hydraulique sur le trajet de l’eau liquide (Kh) diminue alors et tend à freiner le flux d’eau dans la plante, provocant la diminution du potentiel hydrique dans son xylème et les différents tissus qui communiquent avec lui. Peu de données sont malheureusement disponibles sur la forme de la diminution de Kh lors d’une contrainte hydrique. La figure 6A présente quelques-unes de ces données obtenues sur trois espèces de conifères (voir Granier et al., 1989). Pour représenter cette variation, nous avons utilisé une relation présentée sur la figure 6B. La relation présente une forte décroissance en début de dessèchement, plus lente ensuite, puis plus rapide à la fin, en raison de la cavitation et de l’embolie des tissus conducteurs (voir Chap. II.7).
Son équation est la suivante :
(équation 2)
où a, b, c et d sont des constantes issues d’un ajustement statistique.
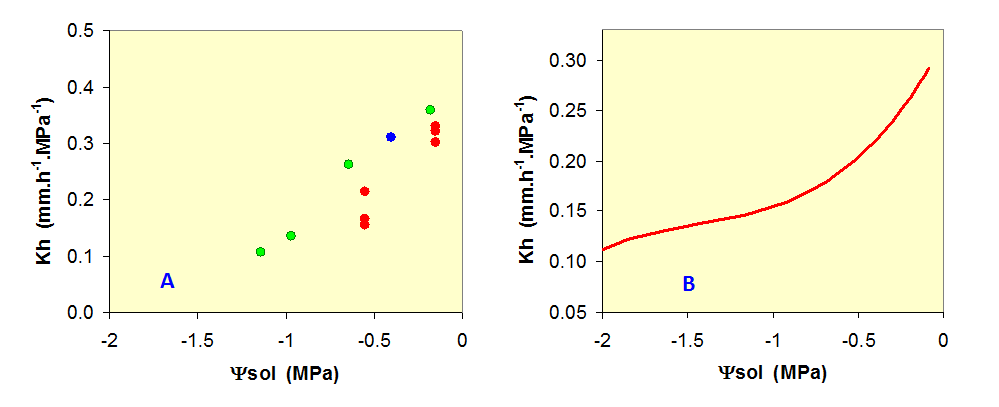
Figure 6. Relation entre la conductance hydraulique totale dans l’arbre (Kh) et le potentiel hydrique du sol. A) mesures réalisées sur des arbres soumis à différents niveaux de sécheresse ( 
: Picea abies, 
: Pinus pinaster, 
: Abies bornmulleriana). D’après Granier et al. (1989) ; B) variations de la fonction utilisée dans le modèle.
Calcul des potentiels hydriques dans l’arbre
Connaissant le potentiel hydrique du sol Ysol et la transpiration T, on peut alors calculer le potentiel hydrique foliaire (Yf) au moyen de l’équation simple ci-dessous (cf. chap. II.6), appelée analogie électrique, qui établit un parallèle avec la loi d’Ohm utilisée en électricité :
, d’où :
(équation 3)
Enfin, si l’on connaît la valeur de la conductance hydraulique des différents tronçons du trajet de l’eau entre le sol et l’atmosphère, il est possible de calculer les potentiels hydriques intermédiaires, notamment dans les tissus de la plante.
Une conséquence de la diminution des potentiels hydriques dans la plante est l’aspiration d’une partie de l’eau contenue dans les « organes-réservoirs » de la plante (voir chap. II.3), qui complémente ainsi le flux de transpiration. Dans ces conditions, certains de ces organes, dits « élastiques » se contractent, phénomène mesurable avec des capteurs spéciaux. La figure 7 donne un exemple de variation de teneur en eau relative d’un organe (TER) en réponse à une variation de son potentiel hydrique. La fonction utilisée dans notre modèle (tirée de Tuzet et al., 2017) est la suivante :
(équation 4)
Dans cette équation, a et p sont des constantes déterminées expérimentalement en desséchant de façon contrôlée des tissus ou des organes de la plante. Noter que la forme de cette courbe est très dépendante de l’organe considéré et de l’espèce.
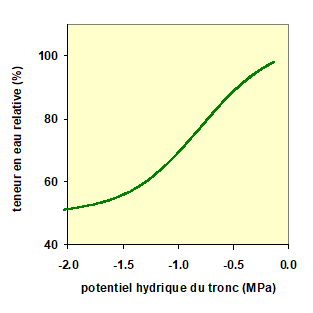
Figure 7. Pour un organe de la plante, par exemple les tissus élastiques du tronc, relation entre sa teneur en eau relative en fonction de son potentiel hydrique (100% : organe à pleine saturation ; 0% : organe totalement desséché).
L’ensemble des fonctions utilisées dans le modèle et représentées sur la figure 2 sont maintenant explicitées. Le modèle est construit et peut être mis en œuvre dans un programme informatique. Nous mettons à disposition une feuille de calcul Excel©, téléchargeable en suivant ce lien, qui permet de réaliser des simulations en faisant varier différents paramètres-clés d’un peuplement forestier : réserve utile du sol, indice foliaire, conductance hydraulique du xylème, volume des réservoirs échangeurs d’eau...
Ce modèle simule des flux et des potentiels hydriques. Il peut être utilisé pour simuler la transpiration en conditions naturelles, l’évolution des potentiels hydriques dans le sol et dans les différents organes de la plante. Ce modèle peut être aussi couplé à d’autres par exemple un modèle de photosynthèse, permettant d’y faire intervenir la régulation de la plante en périodes de contraintes hydriques. Nous présentons ci-dessous quelques simulations.
Sommaire :
