Les trois états de l’eau  

 

Généralités

La matière présente trois états (ou phases) physiques fondamentaux^[1] : gazeux, liquide et solide. Dans les conditions ordinaires de température et de pression existant sur la terre, l’eau se trouve sous ces trois états. Cette caractéristique, particulièrement l’existence d’eau liquide semble rare^[2] dans le système solaire.

Chacun de ces trois états a sa propre organisation moléculaire. Mis à part l’état gazeux, les liaisons H jouent un rôle déterminant dans la structure liquide ou solide. On retrouve dans chaque état les différents mouvements moléculaires (translations, rotations, vibrations) mais leur rythme et leur amplitude sont affectés lors du passage d’un état à l’autre. Les modalités d’arrangement des molécules dans un état donné, à savoir le fait qu’elles soient plus ou moins proches les unes des autres, plus ou moins liées, et dans une configuration plus ou moins ordonnée, déterminent en grande partie les propriétés macroscopiques de cet état (tableau 1).

Etat	Les molécules sont	Conséquences au niveau macroscopique
GAZ Etat non condensé	- désordonnées - espacées - non liées - non liées et très agitées	un gaz est compressible  un gaz n'a pas de volume propre  un gaz n'a pas de volume propre  un gaz se répand dans l’espace
LIQUIDE Etat condensé	- désordonnées  - rapprochées  - peu liées	un liquide est très peu compressible  un liquide n’a pas de forme propre  un liquide s’évapore
SOLIDE Etat condensé	- ordonnées  - rapprochées  - liées	un solide peu avoir une structure cristalline  un solide est incompressible  un solide possède une forme propre

Tableau 1. Comparaison schématique entre un gaz, un liquide et un solide, aux niveaux moléculaire et macroscopique. Par rapport à un solide ou à un liquide, l’état d’un gaz est dit non condensé c’est-à-dire qu’il contient bien moins de matière dans un même volume. Les conséquences de l’arrangement des molécules (colonne du milieu) se traduisent au niveau macroscopique (colonne de droite) ; ainsi, par exemple, du fait que dans un gaz les molécules sont très espacées, un gaz est compressible. De même un liquide n’a pas de forme propre du fait que ses molécules sont peu liées. Lors du passage d’un état à l’autre, la disposition et l’agitation des molécules changent ; par contre leur taille et leur forme ne changent pas. D’après http://phys.free.fr/etats2.htm, modifié.

Dans l’état gazeux (fig. 4a et tab. 1), les molécules sont très éloignées les unes des autres par rapport à leur taille, elles ne sont pas liées mais très agitées ; elles se répandent dans tout l’espace qui leur est offert et peuvent parcourir des distances très grandes (par rapport à leur dimension) avant d’entrer en collision avec une autre molécule. C’est l’agitation thermique, résultant de l’énergie cinétique de chaque molécule, qui est le facteur déterminant de l’organisation des molécules dans un gaz. Cette agitation thermique croît avec la température. Chaque molécule qui rebondit sur une paroi crée une petite force perpendiculaire à cette paroi.  Au niveau macroscopique la somme de ces petites forces se traduit par une pression, elle aussi perpendiculaire à la paroi. La distance entre molécules peut être réduite par pression, c’est ce qui fait qu’un gaz est compressible et qu’il n’a pas de volume propre^[3] : il se répand dans tout l’espace qui lui est offert

Dans l’état liquide (fig. 4b et tab.1), les molécules sont très proches les unes des autres mais elles conservent encore un certain degré d’agitation et leurs positions relatives évoluent continuellement. Il y a donc une certaine organisation moléculaire, en grande partie déterminée par les liaisons H. Mais l’agitation thermique joue aussi, si bien que l’organisation spatiale des molécules conserve un caractère dynamique et extrêmement variable dans le temps et l’espace.

Dans l’état solide (fig. 4c et tab. 1), le degré d’agitation des molécules est réduit à des oscillations autour de positions d’équilibre. Il y a un véritable ordre au niveau moléculaire qui se traduit au niveau macroscopique par une structure cristalline. Une telle structure est constituée par la répétition régulière et dans les trois dimensions, d’un même arrangement (ou motif) moléculaire. La glace a, de ce fait, sa forme propre. Cependant bien qu’étant un corps solide, elle est légèrement compressible.

Le passage gaz Þ liquide Þ solide (et inverse) met en jeu des énergies. D’une façon très schématique, on peut préciser ce qui se passe de la façon suivante. L’énergie totale d’un très grand nombre de molécules peut se décomposer en deux termes : l’énergie cinétique et l’énergie potentielle.

L’énergie cinétique provient des mouvements microscopiques incessants des molécules. Ce terme est étroitement lié à la température du système : il reflète l’agitation thermique des molécules laquelle augmente avec la température. Le second terme est l’énergie potentielle d’interaction qui résulte des forces d’attraction ou de répulsion entre les molécules. Ce terme est d’autant plus important que les molécules sont proches les unes des autres autrement dit que la densité du système est élevée. C’est l’importance relative de ces deux termes qui constitue la base théorique sur laquelle se fait la distinction entre les trois états de la matière. Quand le terme énergie cinétique, due aux mouvements l’emporte largement sur l’énergie potentielle liée aux interactions moléculaires, on a affaire à un gaz ; dans le cas contraire il s’agit d’un solide. Le liquide est un cas intermédiaire et c’est, par là même, le plus difficile à appréhender d’un point de vue théorique.

Pour tous les corps, chacun des domaines gazeux, liquide ou solide dans lequel il peut exister, est délimité par une gamme donnée de température et de pression. Les frontières entre ces domaines sont franchissables : elles correspondent à ce qu’on appelle des changements de phases ou d’état, lesquels nécessitent des conditions très particulières. Pour l’eau, ces passages d’un état à l’autre sont fréquents et intéressent plusieurs aspects de la vie des végétaux. C’est la raison pour laquelle ils sont étudiés ci-dessous.

Rappel : mole et volume molaire.

Avant d’aborder ces changements de phase de l’eau, il faut rappeler une notion fondamentale qui permet notamment, en faisant le pont entre niveaux microscopique, moléculaire, et macroscopique de la matière, de quantifier les échanges d’énergie impliqués dans ces changements. Il s’agit de la notion de mole.

A l’échelle où nous nous situons, nous avons affaire le plus fréquemment à des quantités de matière qui vont le plus sou-vent du microgramme à la tonne. Or les lois de la chimie physique sont souvent définies à partir de grandeurs atomiques ou moléculaires. Il faut donc qu’on puisse passer de ce monde « microscopique » à notre monde « macroscopique ».  La notion de mole est une des voies  principales de ce passage^[4].

La mole est « la  quantité de matière qui contient autant d’entités élémentaires qu’il y a d’atomes dans 12 g de l’isotope 12 du carbone » (Atkins, 2000). De façon plus simple, la mole est un ensemble de 6,022 10²³ molécules, atomes^[5] ou ions (fig. 12). Ce nombre, N_A, est appelé la constante d’Avogadro^[6]. Par exemple, il y a donc 6,022 10²³ atomes de carbone dans une mole de carbone, ou 6,022 10²³ ions de chlore dans une mole d’ions Cl^- et ce même nombre encore dans une mole d’eau. Dans un échantillon qui contient N molécules (ou atomes, ou ions) il y a  donc N/N_A moles.

                                          

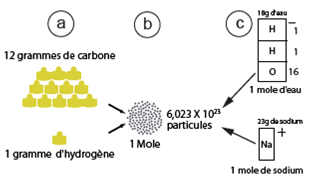
Figure 12. Rappels sur la notion de mole.
a) La mole est, par définition, la quantité de substance contenant le même nombre de particules élémentaires qu’il y a d’atomes dans 12 grammes de carbone ou dans 1 gramme d’hydrogène. Ce nombre est égal à 6,022 10²³ particules. C’est le nombre d’Avogadro.
b) Ces particules peuvent être des molécules, des atomes ou des ions : toutes peuvent être exprimées en moles.
c) 1 g d’hydrogène H, 23 g de sodium Na, 12 g de carbone C ou 18 g d’eau H₂ O, correspondent chacun à une mole de ces différentes substances. D’après K. Smith, 1981.

La masse molaire (on dit aussi masse molaire atomique) d’une substance est la masse d’une mole de cette substance. Elle s’exprime en gramme par mole (g mol^-1). En prenant comme référence la masse molaire de l’atome de carbone (donc la masse de N_A atomes de carbone) et en lui attribuant la valeur de 12 grammes, la masse molaire d’un atome d’hydrogène est alors de 1 gramme, celle de l’atome d’oxygène de 16 grammes et celle de l’eau de 18 grammes (2+16). Ces différentes masses contiennent donc, par définition, 6,022 10²³ molécules chacune (dans la pratique quand on mesure 18 g d’eau au milligramme près, cela signifie que l’on a un nombre de molécules qui est celui de la constante d’Avogadro (à plus ou moins quelques milliards de molécules près !)).

On définit aussi le volume molaire d’une substance, c’est-à-dire le volume occupé par une mole de cette substance. Ce volume dépend de la masse molaire M et de la masse volumique ρ (masse par unité de volume) de la substance. Le volume molaire est donné par la formule : 

                                                           V_m= M/ρ                                                                                 équat. 1

V_m  = volume molaire (cm³ mol^-1)
M   = masse molaire (g mol^-1)
ρ    = masse volumique relative à l’état considéré (g cm^-3) 

La masse volumique de l‘air est établie en prenant :
            78% d’azote N₂(0,78x14gx2) + 21% d’oxygène 0₂(0,21x16g x2) + 1% d’argon (0,01x40g) soit finalement 28,97 g mol^-1 d’air.

Application : pour l’eau liquide : M = 18 g mol^-1 ; ρ = 1,0 g cm^-3 ;
donc le volume molaire (à 20°C) est V_m =  18 g mol^-1 /1,0 g cm^-3  =  18 cm³ mol^-1.

Pour la glace ρ = 0,91 g cm^-3 donc V_m = 18 g mol^-1/0,91 g cm^-3 = 19,78 cm³ mol^-1. On retrouve ce résultat connu que le volume molaire de la glace est supérieur à celui de l’eau liquide, sa densité étant inférieure à celle de l’eau liquide. La glace flotte sur l’eau liquide.

Pour l’eau à l’état de gaz, nous verrons que le volume molaire peut être déduit directement de la loi des gaz parfaits : Vm = 22,4 L.mol-1 à 0°C et à la P atmosphérique normale. On peut alors aussi calculer la masse volumique de l’eau vapeur en inversant l’équation 1 :

                        ρ = M/V_m soit 18/22,4 = 0,8036 g l^-1 (l = litre) ou encore 0,8036 Kg m^-3.

Remarque. La notion de densité est différente de la masse volumique : une densité, pour un corps A est le rapport de la masse volumique du corps A à la masse volumique d’un corps de  référence. Pour les solides et les  liquides, on prend la masse volumique de l’eau à 15°C comme référence ; donc la densité de l’eau est 1 par définition. Pour les gaz on prend généralement l’air. La masse volumique de ce mélange de gaz peut encore être déduite du volume des gaz parfaits en prenant en compte les pourcentages de ses principaux composants :
78% d’azote (N₂) + 21% d’oxygène (O₂) + 1% d’Argon, pèse (0,78x14x2 + 0,21x16x2 + 0,01x40) g,

soit 28,97 g dans 22,4 L à 0°C et 1 atm.

Donc la masse volumique de l’air dans ces conditions vaut 1,293 g.L-1 .

La densité de la vapeur d’eau vaut donc d(vap.eau) = 0,8036 / 1,293 = 0,621

Attention, le mot « density » en anglais est synonyme de masse volumique (et non de densité).

 

L’état gazeux : la vapeur d’eau et sa caractérisation dans l’air.

Le comportement physique d’un gaz réel comme l’eau à l’état vapeur s’appréhende à partir d’un cas plus simple qui sert de modèle : ce modèle s’appelle un gaz parfait. Il s’agit d’un état gazeux « idéal » dans lequel les molécules sont sans volume et sans interaction les unes sur les autres. Le terme énergie potentielle d’interaction est donc nul. L’expérience a montré qu’un certain nombre de gaz réels se comportent, avec une bonne approximation, comme des gaz parfaits, et ce d’autant plus que leur température est basse. C’est le cas en particulier de la vapeur d’eau dans les conditions naturelles.

Pour pouvoir caractériser quantitativement l’état de la vapeur d’eau dans l’air, il faut d’abord rappeler trois notions : les propriétés du gaz parfait « vapeur d’eau », ce qu’on appelle « pression partielle » et « pression de vapeur saturante ».

<La loi des gaz parfaits ou loi de Boyle-Mariotte

Les caractéristiques d’un gaz parfait qu’il faut connaître pour étudier son comportement sont appelées variables d’état. Celles-ci sont au nombre de 3 : le volume, la pression et la température ; leurs valeurs définissent l’état dans lequel se  trouve le gaz. Dans une situation donnée, ces variables d’état ou grandeurs ne sont pas indépendantes les unes des autres : elles sont liées par une relation unique, simple, qu’on appelle l’équation des gaz parfaits ou équation de Boyle Mariotte^[7].

C’est en quelque sorte une synthèse à partir de laquelle il est possible de prévoir et de comprendre le comportement du gaz parfait. Cette loi s’écrit :                                  

                                                                       PV = nRT                                                                     équat. 2

avec en unités du système international (SI) :
P = pression  du gaz  (ML^-1T^-2 ; Pascal)
V = volume du gaz (L³ ; m³)
n = quantité de matière (en nombre de moles)
R = constante, appelée constante des gaz parfaits (voir ci-dessous)
T = température thermodynamique ou température Kelvin (K)

Rappelons que l’échelle de degrés Kelvin est décalée de 273,15 par rapport à l’échelle Celsius (°C). On a donc :

                        Température en K = température en degré C + 273 (si on arrondit)

La figure 13 donne deux représentations de cette loi : i) pour une température donnée, le volume d’une quantité n de gaz est inversement proportionnel à la pression (fig. 13a) ; ii) pour une pression donnée, le volume est une fonction de la température (fig. 13b).

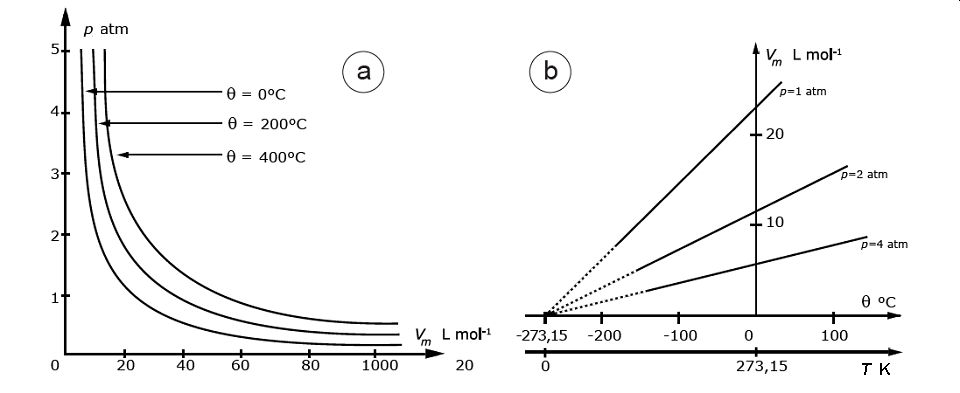
Figure 13. Deux représentations de la loi des gaz parfaits ou loi de Boyle-Mariotte.
a) Courbes dites « pression- volume » à température constante : le volume croît quand la pression décroît ou, plus précisément, le volume est inversement proportionnel à la pression. Chaque courbe (appelée « isotherme » puisqu’elle correspond à une température constante) est une hyperbole, ce qui se traduit par le fait que le produit PV est constant pour tout point d’une même courbe. Tiré de Atkins, 2000.
b) Courbes dites « isobares » donnant la relation linéaire entre le volume d’une mole d’un gaz et la température (en degrés Celsius ou en degré K) pour différentes pressions. Les courbes obtenues se coupent toutes en un point de l’axe horizontal situé à – 273,15°C. Ce point correspond à l’origine de l’échelle des températures utilisées en physique (thermodynamique). C’est le « zéro absolu ». Tiré de Arnaud, 2002.

La seule difficulté dans l’usage de cette équation 2 est le choix des unités.

La constante R a pour équation aux dimensions* « des pressions volume par mole et par degré » comme le montre la relation ci-dessous :

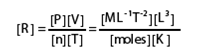                                                                                               équat. 3

L’expression de R est fonction des unités choisies pour exprimer le volume, la pression, la température.

Exemples de valeurs de R :
R = 8,314 Pa m³ mole^-1 K^-1 en SI
Autres expressions de R : 8,314 10^-6 MPa m³ mole^-1 K^-1 ; ou encore 0,08314 bar litre mole^-1 K^-1
ou 8,314 J mole^-1 K^-1 ou 0,08207 litre atm mole^-1 K^-1
RT = 2437 m³ Pa mole^-1 à 20°C ; 24,05 L atm mol^-1 à 20°C
L : abréviation de « litres » ; atm : abréviation pour 1 atmosphère ; 1 atm = 1,013 MPa = 1,013 10_­­⁵ Pa
Pa = Pascals ; MPa = mégaPascals ; K = degré Kelvin

La loi des gaz parfaits permet de calculer une des grandeurs (pression, volume, température, nombre de moles) qui caractérisent l’état d’un gaz dans des conditions particulières, connaissant les trois autres.  

Applications

1) Quelle est la pression dans un récipient de 0,1 m³ qui contient 300 g d’oxygène à 27°C ?

De la relation ci-dessus, on tire P = nRT/V avec n (nombre de moles d’O₂) = 300/32 soit 9,375 moles ;

R = 8,314 (Pa m³ mole^-1 K^-1) ; T = 273 + 27 = 300 K ; V = 0,1 m³. On a donc, après calcul :

P = 233831 Pa soit encore environ 2,3 atmosphères (1.10⁵ Pa = 0,987 atm). Rappel : 1 atm = 1,015 bars

2) Quel est le volume en conditions normales (20°C, 1atm) d’un gaz qui occupe 20 litres à une température de 126°C sous une pression de 6 atm ?

On applique deux fois la relation 2 : la première à 126°C, pour trouver le nombre n de moles du gaz soit :

                        n = (6 atm x 20 litres/399 R) = (6 x 1,013 10⁶ Pa x 0,020 m³) / (399 x 8,314) = 3,658

La seconde fois, à 20°C, pour connaître le volume occupé en conditions normales par ces 3,658 moles :

                        V = nRT/P = (3,658 x 2,437)/1 10⁵ = 0,0891 m³ soit 89 litres environ

3) Quel est le volume molaire d’un gaz parfait dans les conditions standard de température et de pression (soit 20°C^[8] ou 293 K et 1 atm) ?

On a tout de suite (RT donné ci-dessus et P = 1 atm) :

     V_molaire= V_m =  RT/P = RT = 0,08207 x  273,15 = 22,42 L mole^-1 à 0°C sous 1 atmosphère                équat. 4                             

Une mole d’un gaz parfait (à ces températures et pressions moyennes la vapeur d’eau en fait partie) occupe donc environ 22,4 litres à 0°C,  24 litres à 20°C et 25 litres à 25°C.

Remarque : d’un point de vue historique, l’équation 2 a été explorée sous ses différents aspects par différentes personnes, si bien que les noms de plusieurs scientifiques lui sont attachés. Il est intéressant de donner la contribution de Charles^[9] parce qu’elle permet de percevoir la notion de température absolue de façon simple. Charles met au point l’équation 2 en étudiant la relation volume-température à pression constante. Dans ces conditions le volume du gaz est directement proportionnel à sa température : V = nRT/P. Les courbes obtenues sont des isobares (fig. 13b). Elles se coupent toutes au même point de l’axe des températures, dont l’abscisse est égale à -273,15°C. Pour des températures inférieures à cette valeur, on voit que le volume du gaz serait négatif ce qui est impossible. Il s’agit donc là d’une limite absolue de la température. Il est curieux de constater qu’une relation aussi simple que celle de la loi de Charles ait soulevé un problème théorique important, celui de l’existence d’une limite de la température, et conduit à de très nombreuses expériences pour s’en rapprocher toujours plus.

<Les mélanges de gaz : pressions partielles

Dans la plupart des conditions naturelles, on a affaire à des mélanges de gaz et non à des gaz purs. L’exemple le plus commun est l’air, mélange d’un certain nombre de gaz dont les deux principaux sont l’azote (78,1%), et l’oxygène (20,9%) pour l’air sec. L’argon contribue à environ 1%. La contribution de l’eau est grosso modo comprise entre 0,5 et 2% de l’air humide (dont le poids est celui de l’air sec plus celui de la vapeur d’eau) selon le lieu et le climat.

Question : quelle est la contribution de chacun de ces gaz à la pression totale du mélange « air » ? 

Réponse : on définit la pression partielle d’un gaz comme étant celle qu’il aurait s’il occupait, seul, le volume du mélange. La pression totale d’un mélange de gaz est la  somme des pressions partielles de ses constituants. C’est la loi de Dalton^[10] :

                                    Pression partielle du gaz j = (n_j / n_t) x P                                                            équat. 5

n_j = nombre de moles du gaz « j »
n_t  = nombre total de moles de gaz dans le mélange
P = pression totale du mélange
n_j/ n_t = ce rapport s’appelle la fraction molaire du gaz j

Application :

La composition massique de l’air au niveau de la mer est approximativement de 75,5% pour l’azote, 23,2% pour l’oxygène, 1,3% pour l’argon Ar^[11]. Calculer les pressions partielles des constituants sous une pression totale de
1 atmosphère.

Pour appliquer l’équation ci-dessus, il faut calculer la fraction molaire de chaque constituant ce qui suppose de connaître le poids molaire de chacun, à savoir : 28,02 g mole^–1 pour l’azote, 32,00 g mole^–1 pour l’oxygène et 39,95 g mole^–1 pour l’argon. Ces fractions molaires sont indépendantes de la masse totale de l’échantillon de sorte qu’on peut utiliser une masse d’air quelconque pour les calculs, par exemple 100 g. Pour chacun de ces trois gaz, le nombre de moles est proportionnel à leur pourcentage en poids, d’où :

- pour l’azote : (100g x 0,755)/ 28,02 g mole^–1 = 2,694 mol

- pour l’oxygène : (100g x 0,232)/ 32,00 g mole^–1 = 0,725 mol

- pour l’argon : (100g x 0,013)/39,95 g mole^–1= 0,033 mol

On a donc un total de 3,452 moles ; les pressions partielles sont alors :

- pour l’azote : (2,694 / 3,452) x 1 atm = 0,780 atm

- pour l’oxygène : (0,725 / 3,452) x 1 atm  = 0,208 atm

- pour l’argon : (0,033 / 3,452) x 1 atm = 0,009 atm

Ces calculs ne supposent pas que les gaz soient parfaits car la relation 5 ci-dessus est valable pour tous les gaz. Noter qu'on retrouve bien les pourcentages volumiques de chacun des gaz constitutifs.

<Pression de vapeur saturante ou non saturante

L’expérience illustrée figure 14 permet de comprendre aisément ces deux notions.
Supposons que nous disposions d’un récipient aux parois de verre (rigides et transparentes) d’un volume fixe de
1 litre et possédant deux entrées, l’une permettant d’y injecter, par très petites doses, de l’eau liquide, l’autre reliée à un manomètre. Tout le dispositif est maintenu à une même température, Ta = 25°C par exemple. Au départ l’air du récipient est de l’air sec, sans vapeur d’eau.

 

 

 

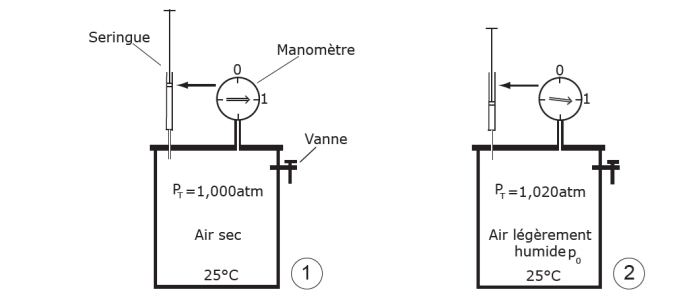
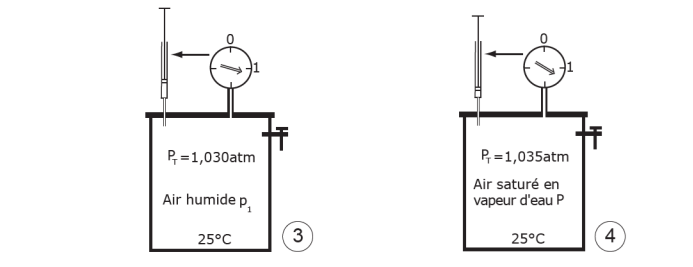
Figure 14. Pression de vapeur saturante et pression non saturante. Le dispositif représenté sur la figure illustre la signification de ces deux notions. Considérons une enceinte à température constante arbitraire (25°C par exemple) munie d’un manomètre qui contient de l’air sec à la pression atmosphérique (soit 1013h Pa, étape 1). Introduisons une petite quantité d’eau liquide à l’aide d’une seringue. Cette eau se vaporise immédiatement, ce qui entraîne une augmentation de la pression totale P_T. En effet la vapeur d’eau introduite exerce une certaine « pression de vapeur » proportionnelle à la quantité d‘eau introduite (p pour l’étape 2, p₁ pour l’étape 3, et P  pour l’étape 4). Il y a aussi une petite diminution de la température puisqu’il y a eu évaporation (voir § IV). Nous n’en tenons pas compte ici. La quantité de vapeur d’eau que l’on peut ainsi introduire est limitée. On constate en effet qu’au delà d’une certaine quantité, la pression n’augmente plus et l’eau reste sous forme liquide (4) : l’enceinte est saturée. Cette quantité d’eau maximale que l’air peut accepter croît avec la température, comme le montre la figure 15. Par ailleurs on remarquera que les valeurs de pression de vapeur d‘eau sont très faibles par rapport à la pression atmosphérique, laquelle est principalement due, conformément à la loi de Dalton, à l’azote et à l’oxygène. Si on avait fait le vide dans l’enceinte avant d’y introduire progressivement de l’eau, celle-ci se serait vaporisée de la même façon, et la pression de vapeur saturante y serait quasiment la même.

Étape 1 : on commence par injecter un tout petit volume d’eau liquide, quelques mg. Il se volatilise tout de suite ; en même temps la pression totale P_T (air + vapeur d’eau) augmente un peu dans le récipient : cette pression résulte de l’injection de molécules d’eau, qui se sont vaporisées dans le récipient. L’agitation continuelle de ces molécules, et leurs collisions contre les parois, génèrent une pression qu’on appelle pression de vapeur p. C’est la pression partielle de vapeur d’eau. En répétant cette expérience (étapes 2 et 3) on obtient des couples de valeurs : quantité d’eau injectée n, et pression p. Etant donné que la température est constante, on pourrait vérifier, comme l’indique la loi des gaz parfaits vue ci-dessus, que la relation entre n et p est linéaire, c’est-à-dire que la pression de la vapeur d’eau (p, p_1, puis P) est bien proportionnelle à la quantité de vapeur d’eau présente dans le récipient.

Étape 2 : au bout d’un certain nombre d’injections, on voit que de l’eau liquide apparaît en bas du récipient et que la pression n’augmente plus. La valeur de cette pression particulière s’appelle la pression de vapeur saturante ; on la note P. Elle correspond à la plus grande quantité de vapeur d’eau qui peut être contenue dans le volume de ce récipient à une température donnée : si l’on continue d’en ajouter, cette eau se condense en eau liquide et forme un film au fond du récipient.

Étape 3 : si maintenant on répète l’expérience sur toute une gamme de températures et qu’on ne conserve que les valeurs de la pression de vapeur saturante P, on voit que celle-ci augmente avec la température selon une loi représentée par la courbe de la fig.15. C’est la courbe de pression de vapeur saturante en fonction de la température exprimée en degrés Celsius (°C).

Remarque. 0n voit que les valeurs de cette pression de vapeur saturante correspondent, pour les températures ordinaires de l’air, à des valeurs très faibles (1 à 2 kiloPascals) en comparaison de la pression de l’air qui est d’environ 100 kiloPascals.

En considérant que la vapeur d’eau est un gaz parfait, sa pression de vapeur est donnée par l’équation des gaz parfaits : p (ou P) correspond à la pression dans l’équation des gaz parfaits écrite comme suit :

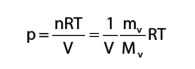                                                                 équat. 6                                                                           

p = pression de vapeur (Pa ou MPa) ou P s’il s’agit d’une pression de vapeur saturante de l’air

n = nombre de moles de  vapeur d’eau dans le volume V (nombre sans dimension)

m_v = masse de vapeur présente dans le volume V (kg)

M_v = masse molaire de l’eau (18 10^-3 kg.mol-1)

V  = le volume d’air humide considéré (m³)

R =  constante des gaz parfaits (voir équat.2)

T = la température (en degré K)

Application : voir plus loin le calcul de la masse de vapeur d’eau dans l’air.

<Caractérisation de l’état de la vapeur d’eau dans l’air : pression de vapeur, humidité relative, point de rosée

Avec l’aide de la courbe de la figure 15, on peut maintenant comprendre deux des nombreuses grandeurs qui servent à définir l’état de la vapeur d’eau dans l’atmosphère mais aussi, en partie, les relations entre l’air et les surfaces végétales : il s’agit de l’humidité relative (notée HR) et de la température du point de rosée

Humidité relative

Plaçons nous au point A de la figure 15 : imaginons qu’il représente un petit volume fermé d’air humide, dont la pression de vapeur est p et la température T.  Refroidir ce petit volume en conservant ces pressions revient à déplacer
le point A sur une parallèle à l’axe des températures. Ce volume finit par atteindre la courbe de pression de vapeur saturante P(T_air). En ce point, la pression de vapeur de l’air du volume fermé devient une pression de vapeur saturante ; la température correspondante de ce point particulier s’appelle la température du point de rosée, T_rosée.

 

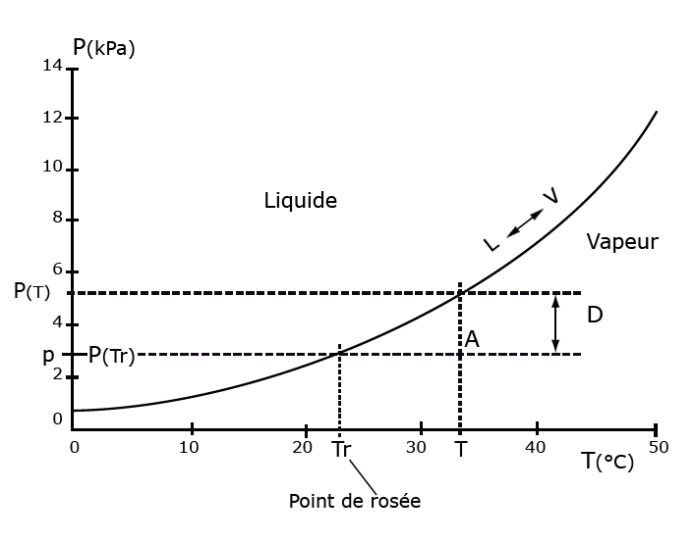
Figure 15. Courbe de la pression de vapeur saturante de la vapeur d’eau, (P), en fonction de la température (T) et définition du point de rosée.
On représente par un point A une petite quantité de vapeur d’eau, que l’on refroidit : au départ elle occupe un petit volume d’air à une température T (environ 33°C) et à une pression de vapeur p (voisine de 3kPa). On suppose que l’ensemble se refroidit en restant à la même pression, comme cela peut arriver dans une atmosphère immobile au cours de la nuit ; la trajectoire de la vapeur d’eau est donc parallèle à l’axe des températures jusqu’à atteindre la courbe des pressions de vapeur saturante (courbe L « V). A cet endroit sur la courbe, la pression de vapeur p devient aussi la pression de vapeur saturante correspondant à une certaine température, appelée température du point de rosée (Tr). La double flèche (D) indique pour la température, T (environ 33°C), de ce volume d’air, la valeur du déficit de saturation défini par  D = P(T) – P(Tr). D’après Lagouarde et al, 1996.

La température du point de rosée est donc la température pour laquelle la pression de vapeur de l’air devient saturante.

L’humidité relative HR est le rapport (multiplié par cent) entre la pression de vapeur d’eau dans l’air et la pression de vapeur saturante à la même température :            

                                                           HR = 100 p/ P(T_air)                                                                      équat.  7           

HR = humidité relative en %

p = pression de la vapeur d’eau dans l’air (Pa ou MPa) à la température T_air

P = pression de vapeur saturante à la même température de l’air, T_air

Sur la figure 15, on voit que chaque valeur p peut-être considérée comme une pression de vapeur saturante P, d’une température particulière appelée point de rosée. On peut donc, dans la formule ci-dessus, remplacer p par la même pression de vapeur d’un certain point de rosée P(T_rosée). L’expression de l’humidité relative HR s’écrit donc aussi sous la forme :

                                                           HR = 100 P(T_rosée) /P( T_air)                                                             équat. 7’

La valeur 0% correspond à un air parfaitement sec et 100% à un air saturé en vapeur d’eau.

On  appelle déficit de saturation de l’air le complément à 100 de l’humidité relative :

                                                    D = 100 – HR= 100 [1- P(T_rosée) / P(T_air)                                            équat. 8                                                                                                              

Le déficit de saturation varie donc de 0 (air complètement humide, aucun déficit) à 100 (air complètement sec, déficit maximal).                                                                    

L’expression de HR (équat. 7) montre que l’humidité relative de l’air peut varier de deux façons :

- soit parce que la température de l’air augmente : p reste la même mais P(T_air) augmente puisque T_air augmente, donc HR diminue

- soit parce que, pour une même température de l’air T_air, la quantité de vapeur d’eau dans l’air augmente (irrigation, pluie, changement de la masse d’air) d’où une élévation de p = P(Tr) ; HR augmente.

L’augmentation de l’humidité relative HR ne signifie pas toujours un enrichissement de l’air en vapeur d’eau : par exemple, un même volume d’air à 18°C ayant une HR de 60% contient plus de vapeur d’eau que le même volume à -5°C dont l’HR est de 80% (cf. tab. 2). De même deux valeurs égales d’HR ne correspondent pas nécessairement à une même quantité de vapeur d’eau dans l’air (cf. tab. 2). Pour être certain de conclure sur l’enrichissement ou l’appauvrissement en eau de l’air à partir de la comparaison des valeurs de HR, il faut que la comparaison se fasse à une même température de l’air.

Cas	Conditions	Températures en °C	Humidité absolue (masse d’eau en g par kg d’air sec)
A	A l’extérieur en hiver : HR = 80%	- 5°C	2,1
B	Dans un local : HR = 60%	18°C	7,8
C	Dans un local : HR = 60%	20°C	8,8
D	A l’extérieur, en été : HR = 70%	25°C	14,0

Tableau 2. Exemples de valeurs d’humidité relative (ou degré hygrométrique) à différentes températures et dans différents cas (de A à D). Les cas illustrés dans ce tableau sont resitués figure 16. On remarquera ; i) que plus l’air est froid plus une même valeur de HR peut être obtenue avec une quantité d’eau faible ; ii) qu’une augmentation de l’humidité relative HR ne signifie pas toujours un enrichissement de l’air en vapeur d’eau : comparer le premier cas (A) avec les autres (B, C, et D). On retiendra que l’on ne peut comparer des HR (pour en conclure que l’air est plus humide ou plus sec dans un lieu que dans un autre) que si la température est la même dans les cas comparés. Source : http://energie.wallonie.be/energieplus

Remarque : le fait que l’air humide est plus léger (on devrait dire moins dense) que l’air sec semble parfois aller à l’encontre du « bon sens ». Pour comprendre pourquoi ce n’est pas le cas, on peut se rapporter à la loi des gaz parfaits (équat. 2). Celle-ci indique qu’à une même pression et pour une même température, un volume donné de gaz contient le même nombre (n) de molécules d’un même gaz ou de plusieurs. Si donc on ajoute quelques moles d’eau à un volume donné d’air, pour que la pression ne change pas, le même nombre total de moles d’oxygène et d’azote doit être retiré. Avec un poids molaire de 0,018 kg par mole, la mole d’eau pèse moins que les moles qu’elle remplace : 0,032 kg par mole pour les molécules d’oxygène O₂ et 0,028 kg par mole pour les molécules d’azote N₂. La densité du volume d’air humide est donc inférieure à celle du même volume d’air plus sec. On peut retenir qu’aux températures ordinaires, même dans un air saturé en vapeur d’eau, l’eau ne représente qu’à peu près 2 ou 3% des molécules présentes ou de la masse d’air : par conséquent, il en est de même des pressions partielles de la vapeur d’eau. 

Application : quelle est la masse de vapeur d’eau contenue dans 1 m³ d’air à 20°C et dont l’HR est de 50% ?

C’est encore un cas d’utilisation de l’équation 2 des gaz parfaits, légèrement modifiée pour convertir le nombre de moles de vapeur d’eau (n) en masse (m_v) :

n = masse totale de vapeur d’eau, m_v / masse molaire de la vapeur d’eau, M_v

Il faut commencer par déterminer à quelle pression de vapeur d’eau correspond une HR de l’air de 50% à 20°C. Les tables de vapeur saturante P en fonction de la température donnent P(T₂₀) =  2339 Pa ; donc pour une HR = 50% la pression de vapeur est 1169,5 Pa. On peut maintenant appliquer la relation 6 (en faisant attention aux unités !). On obtient la valeur de la masse d’eau, m_v, en prenant pour valeur de RT à 20°C, RT= 2437 m³ Pa mole^-1

                                   

Sachant qu’un m³ d’air sec à 20°C pèse 1,204 kg, rapportée non plus au volume mais à 1 kg d’air sec, la quantité de vapeur d’eau dans 1 kg d’air sec est donc de 8,638 / 1, 204 = 7,17 g. C’est à peu près la valeur donnée par la fig. 16.

On retrouve aussi la donnée déjà signalée : la vapeur d’eau dans l’air ne représente qu’environ 1% de la masse de l’air dont les trois gaz principaux (azote, oxygène, et argon) représentent plus de 99%. Cependant la quantité de vapeur d’eau dans l’air est très variable, celle de l’argon non. Quant au gaz carbonique, sa « teneur » est exprimée, le plus souvent, en partie par millions (ppm) en volume : la valeur actuelle est de 380 ppm soit donc, grossièrement, dix fois moins que la vapeur d’eau.

                       ‘

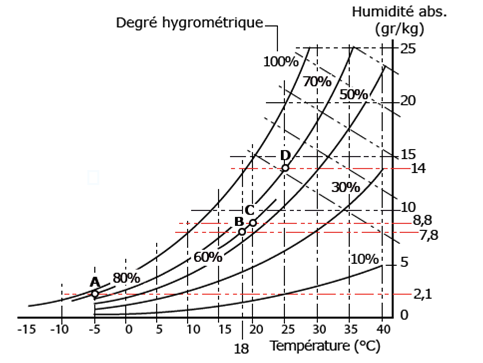Figure 16. Diagramme donnant pour différentes températures de l’air, la correspondance entre humidité relative (HR) ou degré hygrométrique de l’air (exprimés en %) et humidité absolue. L’humidité absolue est la quantité de vapeur d’eau dans l’air ; elle s’exprime en grammes d’eau par kilo d’air sec. Les cas illustrés dans le tableau 2 sont situés dans ce diagramme (mêmes lettres A à D). On voit que plus l’air est chaud, plus une même HR correspond à des valeurs importantes d’eau dans l’air : par exemple, cas B, une humidité de 60% correspond à 7,8 grammes d’eau vapeur par kilo d’air sec mais à 8,8 grammes si l’air est à 20°C. Source : http//energie.wallonie.be/energieplus

 

L’état liquide : l’eau, un liquide très particulier

L’état liquide possède certaines des propriétés la rapprochant de l’état gazeux et d’autres de l’état solide.

Comme l’état gazeux, l’état liquide est soumis à l’agitation thermique qui confère aux molécules des mouvements désordonnés, très rapides et incessants : c’est le mouvement brownien, découvert en 1827 par Brown (cf.note 9), en suivant au microscope les mouvements de grains de pollen dispersés à la surface de l’eau. Comme l’état solide, l’état liquide est un état dit condensé, c’est-à-dire que les molécules restent voisines les unes des autres, plus ou moins « tassées ». Néanmoins les molécules d’eau conservent une certaine mobilité à très courte distance et forment entre elles, grâce aux liaisons H, des associations extrêmement éphémères mais toujours recommencées, comme signalé plus haut. Cet arrangement a deux conséquences : d’une part, un liquide, comme un gaz, n’a pas de forme propre ; d’autre part, cette très grande proximité des molécules fait qu’un liquide est pratiquement incompressible (le doublement de pression de 1 à 2 bars ne réduit le volume de l’eau que de 0,01%). Cette quasi incompressibilité fait que l’eau transmet les pressions. Nous verrons que cette propriété est essentielle pour comprendre les mouvements de l’eau à travers le végétal (chap. II.6, II.7, II.8 et II.9).

Des trois états de la matière, l’état liquide est celui qui est le plus difficile à comprendre à partir des interactions moléculaires. On ne sait d’ailleurs pas encore décrire d’une façon précise et satisfaisante, sur une échelle de temps un peu longue, les positions dynamiques de ne serait-ce que quelques milliers de molécules d’eau. Pour notre propos, disons qu’à un instant donné, toutes les molécules d’eau sont liées car le nombre de liaisons H est très grand. Mais, dans une masse liquide, il y a des régions plus denses que d’autres, dans lesquelles se constituent des sortes d’amas particuliers. Ceux-ci n’ont pas de cohérence, en ce sens qu’ils ne se maintiennent pas dans le temps, mais changent continûment, toutes les picosecondes (10^-12 s) environ. En moyenne, une molécule d’eau est toujours entourée de 4 à 5 molécules d’eau. Ce nombre s’abaisse avec la température, approchant 4 qui est la  valeur pour  la glace (fig. 3b).

Lorsque la température augmente, deux effets contraires interagissent. D’une part, l’agitation thermique dilate l’eau, ce qui tend à faire diminuer sa densité. D’autre part, le nombre de liaisons H décroît ce qui tend à rapprocher les molécules et ainsi à faire croître la densité. Le résultat global est en faveur d’une augmentation de densité entre 0°C et 3,8°C en raison du nombre important de liaisons H rompues (la structure de la glace s’effondrant), et d’une diminution de densité au-delà de 3,8°C, l’agitation thermique l’emportant (fig. 17). Autrement dit contrairement à l’immense variété des corps, solides, liquides ou gaz qui se dilatent quand on les chauffe, l’eau au contraire se contracte quand on la chauffe entre 0°C et 3,8°C. A cette température de 3,8°C, elle est donc plus dense qu’à 0°C.

                                             

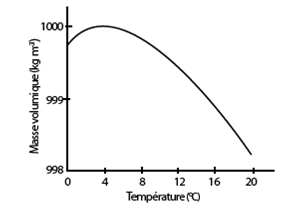
Figure 17. Variation de la masse volumique de l’eau avec la température, entre 0 et 20°C. La résultante des forces attractives (interactions moléculaires et liaisons H) et répulsives (agitation thermique) entre les molécules d’eau explique les variations de masse volumique de l’eau liquide en fonction de la température. On remarquera le maximum de masse volumique à 3,8°C suivi de sa chute de quelques décigrammes (999,97kg m^-3 à 4°C, et 999,84 à 0°C. Par ailleurs à partir de 4°C environ, la masse volumique de l’eau diminue constamment avec l’augmentation de la température. Voir aussi la fig. 29. Attention à l’effet « dilatation » de l’axe des masses volumiques. D’après Kane et Sternheim, 1986.

<Quelques  propriétés physico-chimiques de l’eau liquide

L’eau liquide possède un grand nombre de propriétés chimiques, en particulier liées à l’agencement de ses molécules. Ces propriétés ne sont pas développées ici du fait de l’orientation de cet ouvrage. Elles jouent cependant un rôle essentiel dans la physiologie des plantes. Les plus importantes sont donc rapidement présentées ci-dessous. On trouvera dans les ouvrages de biochimie et de biologie cellulaire des développements plus amples à leur propos.

Viscosité

Cette propriété des fluides sera examinée dans le chapitre IV. Elle est citée ici simplement en tant que propriété de l’eau liquide.

La viscosité quantifie la résistance à l’écoulement ; c’est le contraire de la fluidité. Un liquide qui s’écoule facilement a une faible viscosité : c’est le cas de l’essence. Les huiles, le miel, par contre s’écoulent plus difficilement : leur viscosité est forte. La viscosité est liée à la dissipation d’énergie par frottement au sein du fluide. Ces frottements dépendent de l’existence et de la nature des interactions moléculaires (donc des liaisons H), de la grosseur des molécules constitutives du fluide (en général les grosses molécules se dégagent difficilement les unes des autres) et de la température.

La viscosité de l’eau et ses variations selon la température sont des particularités très importantes pour les plantes. Cette viscosité décroît rapidement avec l’augmentation de la température : elle chute de plus de 45% entre 5°C et 30°C (fig. 18). Comme on le verra au chap. II.4, ce fait a une grande importance pour l’absorption racinaire.

   

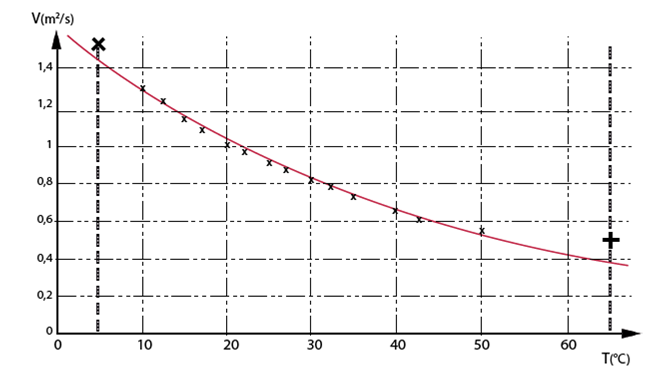
Figure 18. Variation de la viscosité de l’eau avec la température. La viscosité traduit la plus ou moins grande facilité d’un liquide à s’écouler : par exemple le miel est bien plus visqueux que l’eau. On voit que cette viscosité (il s’agit de la viscosité dynamique exprimée en 10^-6 m²s^-1) décroît rapidement avec la température. Elle joue un rôle non négligeable dans l’absorption racinaire (chap. II.4). Source : http://www.ac-nancy-metz.fr/enseign/physique/

 

Solubilité des gaz dans l’eau

La solubilité d’un gaz dans un liquide (appelé dans ce cas solvant) dépend de quatre facteurs : la nature du gaz dissous, celle du solvant, de la température et de la pression. La solubilité met en jeu des forces d’attraction ou de répulsion entre les molécules du solvant et du soluté. Elle décroît avec l’augmentation de la température qui tend à rompre les liaisons gaz-solvant (agitation thermique). La solubilité des gaz dans l’eau augmente au contraire avec la pression.

Le tableau 3 donne quelques valeurs de solubilité de gaz courants dans l’eau à différentes températures. On remarquera : i) la grande solubilité du gaz carbonique par rapport à l’oxygène et celle extrêmement élevée de l’ammoniac ;

ii) la décroissance de la solubilité avec l’augmentation de température ;

iii) la faible solubilité de l’air, et des principaux gaz qui le constituent.

On verra au chapitre II.9 les conséquences de cette solubilité à propos de la composition de la sève « brute » en provenance du sol.

Nature du gaz dissous	°C	20°C
Hydrogène  (H2)	0,0215	0,0182
Oxygène  (O2)	0,0489	0,0310
Gaz carbonique (CO2)	1,7130	0,8780
Azote (N2)	0,0235	0,0154
Ammoniac (NH3)	1049	730
Air	0,0288	0,0187

Tableau 3. Exemples de valeurs de solubilité de quelques gaz dans l’eau à deux températures, à la pression atmosphérique normale (en litre de gaz dissous par litre d’eau). On notera :
i) la faible solubilité de l’air et des gaz qui le constituent.
ii) la très grande solubilité de l’ammoniac (donnée ici pour montrer la gamme très étendue des solubilités possibles).
iii) la décroissance de la solubilité avec la température. D’après Kiréev, 1975.

Solubilité des solides dans l’eau

L’eau est un des solvants les plus efficaces pour dissoudre les composés ioniques ou polaires du fait de la capacité de ses molécules à s’entourer d’autres molécules chargées électriquement (cf. §II.3), en particulier les ions (fig. 9 et 19). C’est vrai aussi pour un très grand nombre d’autres corps chimiques comportant des radicaux capables de former des liaisons H avec l’eau. Par exemple le saccharose, (sucre de table) comporte des radicaux appelés groupes hydroxyles (OH^-).

Plongé dans l’eau il va rapidement se dissoudre c’est-à-dire que les molécules de saccharose vont s’entourer complètement de molécules d’eau établissant des liaisons H avec leurs groupes hydroxyles. Cette espèce de coque hydratée que forme ainsi l’eau autour des molécules de saccharose empêche des agrégats de sucre de s’édifier. C’est donc bien cette possibilité de former des liaisons hydrogène avec l’eau qui fait la différence entre les molécules polaires « hydrophiles » et les molécules non polaires « hydrophobes » comme les huiles. Un grand nombre de macromolécules biologiques polaires en solution (protéines, sucres, acides nucléiques) sont donc entourées par des molécules d’eau qui forment autour d’elles un volume « d’hydratation » plus ou moins important. Ces molécules d’eau sont dissociées de l’eau en tant que solvant puisqu’elles sont associées aux macromolécules^[12].

 

 

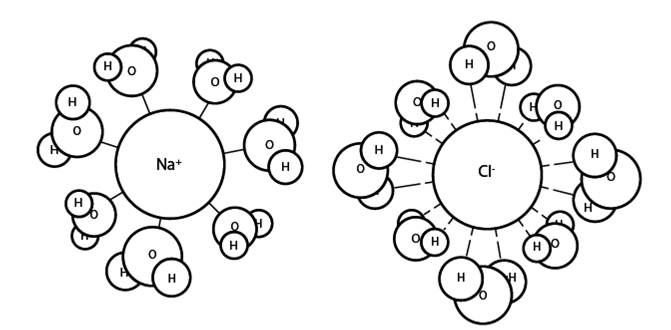
Figure 19. Schéma montrant le rôle de l’eau en tant que solvant. Exemple d’une solution de chlorure de sodium. Les ions chlore (Cl^-) et sodium (Na⁺), sont entourés par une couche d’hydratation formée de molécules d’eau dont l’orientation dépend de la nature, anion (chargé négativement) ou cation (chargé positivement) de  l’ion. Voir aussi fig.11.

Contrairement aux gaz, la solubilité des solides augmente généralement avec la température mais il existe de nombreuses exceptions : la solubilité de certains corps peut en effet décroître avec la température ou même ne varier que très peu avec elle (c’est la cas pour le chlorure de sodium Na Cl).

Le tableau 4 donne des exemples de solubilité dans l’eau de quelques corps chimiques.

Soluté	Solubilité en grammes par litre	Température
Chlorure de sodium	365	°C ; 384 à 80°C
Iodure de sodium	1840	25°C
Sulfate de cuivre	316	°C
Saccharose	1790	°C ; 1970 à 20°C
Urée	780	°C

Tableau 4. Exemples de solubilité de quelques solides dans l’eau. On remarquera l’extrême solubilité de certains corps comme le iodure de sodium et le saccharose. En général contrairement à ce qui se passe pour les gaz, la solubilité des solides augmente en général, quoique légèrement, avec la température.  Sources : Kirèev, Wikipedia.

L’eau a une chaleur spécifique (ou capacité thermique massique) élevée.

La chaleur spécifique (ou chaleur massique) c, d’un corps, est la quantité de chaleur nécessaire pour élever d’un degré Celsius (ou Kelvin) la température de l’unité de masse de ce corps. On peut dire aussi qu’elle rend compte de la capacité d’un corps à stocker de la chaleur. La chaleur spécifique de l’eau est de c = 4185 J kg^-1 K^-1 à 0°C ou (273 °K) : elle s’exprime donc en joules par kilogramme et par degré Celsius ou Kelvin. Exprimée en calories, c  vaut 1000 (par définition de la calorie ; 1 calorie = 4,185 J) : il faut donc 1000 calories pour élever
1 kilogramme d’eau de 1 degré. Cette valeur est élevée par rapport aux valeurs de chaleur spécifiques d’autres corps ; elle est en relation avec le fait qu’il faut briser des liaisons H pour élever la température. La chaleur spécifique varie légèrement avec la température et la pression mais plus encore avec l’état physique. Ainsi la chaleur spécifique de la glace n’est plus que c = 500 calories par kilogramme de glace (entre 0 et -10°C) soit encore
2089 J kg^-1 K^-1.

Cette valeur importante de la chaleur spécifique permet à l’eau de « stocker » la chaleur et du même coup d’atténuer les variations de température : s’il faut fournir beaucoup de chaleur pour élever la température de l’eau liquide, inversement cette eau pourra en restituer beaucoup sans baisse importante de sa température propre. Ainsi s’explique le rôle tampon que joue la mer sur les climats côtiers.

Ionisation de l’eau, pH d’une solution aqueuse^[13]

L’eau pure, même distillée, conduit le courant électrique ; cela signifie que des ions sont présents. Ceux-ci proviennent de la dissociation d’une infime proportion de molécules d’eau selon le schéma ci-dessous :

                                                                H₂O  Û H⁺   +  OH^-                                                                        réaction 1

 H⁺ est un proton et OH^- est un hydroxyde.

La dissociation d’une molécule d’eau consiste en la rupture de l’une des liaisons H-O. L’ion H⁺ (ou proton) formé se combine rapidement avec une molécule d’eau pour former un ion hydronium, H₃ O⁺. On peut donc aussi écrire la dissociation de l’eau sous la forme ci-dessous (appelée autoprotolyse de l’eau) bien qu’on convienne cependant de raisonner en concentration de protons H⁺.

                                                               2 H₂O  Û H₃ O⁺  +  OH^-                                                                        réaction 1bis                                                                            

On voit donc que l’eau peut produire des protons et des OH-, et donc, suivant le contexte, se comporter soit comme une base soit comme un acide. On dit que la molécule d’eau est amphotère.

Remarque. Les écritures H₃O⁺, H⁺, etc, sont des écritures conventionnelles. Tous les ions présents dans une solution sont « solvatés » c’est-à-dire liés à un nombre plus ou moins grand de molécules d’eau. Les réactions 1 et 1bis sont donc équivalentes pour la définition du pH.

Dans l’eau (très) pure, les deux ions, proton H⁺ et hydroxyde OH^- sont en concentrations égales, conformément au fait que, globalement, l’eau est électriquement neutre. Les mesures montrent que, dans ces conditions, la concentration de chacun de ces ions est de 10^-7 moles par litre à 25°C. Donc dans l’eau très pure :

                               [OH ^-] = [ H₃O⁺ ] =  10^-7 mol litre^-1 à 25°C

Dans l’eau pure il y a donc autant d’ions positifs (ou cations) que d’ions négatifs (ou anions). Cette situation se caractérise en disant que le « pH » ou (potentiel hydrogène) de l’eau est neutre, la définition du pH étant la suivante :

on appelle pH^[14] d’une solution aqueuse l’opposé du logarithme décimal de la concentration en cations H⁺, exprimée en moles  par litre^32b :

                                           pH = log  (1/ [ H₃O⁺] = colog [H₃O⁺ ] = - log [H₃O⁺]

Pour l’eau pure à 25°C, le pH est égal à - log 10^-7 = 7. Pour des solutions contenant des ions positifs et négatifs en quantités inégales (par exemple une solution d’acide chlorhydrique, de soude ou d’ammoniac), le pH ne sera  plus neutre, mais « acide » ou « basique ». Sa valeur sera différente de 7. Les solutions acides libèrent des ions H⁺. On peut en effet dire qu’un acide est une substance qui se dissocie dans l’eau en donnant des ions H⁺. Une base est au contraire une substance qui se dissocie dans l’eau en donnant des ions OH^- . Dans les solutions acides, la concentration en H⁺ est donc plus grande que dans l’eau pure ; cette concentration augmente avec l’acidité : les valeurs du pH sont inférieures à 7 (attention, le pH diminue quand la concentration en H⁺ augmente). Contrairement aux solutions acides, les solutions basiques (on dit aussi alcalines) fixent (plus ou moins complètement) les ions H⁺ (Arnaud 2002). Ceux-ci ne sont plus tous libres, comme dans l’eau pure. En conséquence, dans les solutions basiques les concentrations en H⁺ sont plus petites que dans l’eau pure. Elles diminuent au fur et à mesure que l’alcalinité augmente, une base forte fixant plus de protons H⁺ qu’une base faible. Les valeurs du pH sont donc supérieures à 7 (fig. 20).

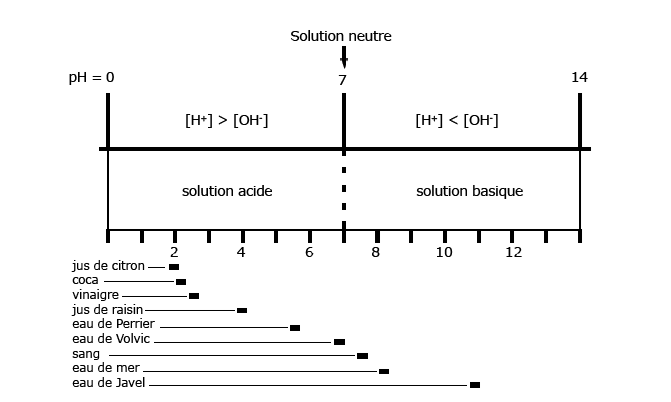
Figure 20. Échelle de pH de l’eau ou d’une solution. Dans une solution, mais aussi dans l’eau pure, il y a toujours des molécules d’eau dissociées en ions H⁺ (appelés protons) et OH^{- (}appelés hydroxydes). Dans l’eau pure la concentration de ces deux ions est la même : l’eau est « neutre » c’est à dire ni acide ni basique. Au contraire dans une solution « acide » il  y aura plus de protons que dans l’eau pure, car les solutions acides libèrent des protons : leur concentration est donc supérieure à celle de l’eau pure. Par contre, dans une solution basique, la concentration des ions H⁺ est inférieure à celle de l’eau pure. Le pH est une grandeur fonction de cette concentration des ions H⁺ ou protons, par conséquent une mesure du caractère acide ou basique d’une solution. Il est égal à l’opposé du logarithme de la concentration en protons. Ainsi, plus il y a de protons plus le pH est faible et la solution acide ; moins il y a de protons, plus la solution est basique et plus le pH est grand. Quelques exemples de pH sont donnés. Source : http://e.m.c.2.free.fr

L’échelle des pH pour les solutions aqueuses est pratiquement limitée à l’intervalle 0-14^[15]. Quand  une solution devient 10 fois plus acide son pH diminue d’une unité ; si elle devient 100 fois plus acide, le pH diminue de 2 unités.

La capacité de l’eau à transporter les protons H⁺ est très importante du point de vue biologique. Ceux-ci jouent un rôle essentiel dans tout le fonctionnement du vivant donc en physiologie végétale. Ils interviennent dans de nombreuses réactions chimiques (les réactions acido-basiques) et dans des processus biologiques tels que l’action des enzymes et les échanges cellulaires. Ainsi par exemple, il existe des protéines spéciales (appelées pompes à protons) qui fonctionnent de façon à enrichir les cellules en protons. Aujourd’hui, on ne sait pas encore expliquer d’une façon sûre par quels mécanismes les protons diffusent dans l’eau, même si l’on sait que ce sont les espèces chimiques qui diffusent le plus rapidement.

 

Pression dans un gaz et dans un liquide.

<Généralités sur la notion de pression

Quand on parle de pression, on pense souvent à une force qui s’exerce contre quelque chose, par exemple un gaz sur les parois d’une enceinte. De même si nous tirons un objet nous exerçons une force sur lui. Les forces sont caractérisées par une grandeur et une direction.

La pression et la force sont deux grandeurs physiques distinctes, qui sont cependant liées en ce sens que la pression est  une force appliquée par unité de surface.

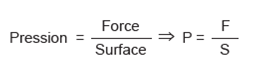                                             équat. 9                                                                                                                                                                 

F = Force (MLT^-2 ; newtons)
S = Surface (L² ; m²)
P = Pression (ML^-1T^-2 ; pascals)

Dans le Système International, les forces s’expriment en newtons (abréviation N) : un newton est la force capable de communiquer à une masse de 1 kilogramme une augmentation de vitesse de 1 mètre par seconde chaque seconde.

Remarque : il existe une différence importante entre les fluides et les solides en ce qui concerne les forces et des pressions. Les solides (indéformables) transmettent intégralement les forces alors que les liquides transmettent intégralement les pressions (fig. 21). Cette figure 21 fournit l’occasion de rappeler la différence entre masse et poids qui va être utilisée ci-dessous. 

 

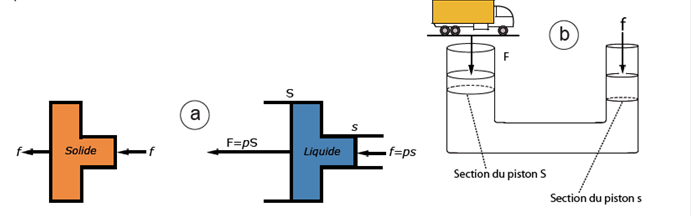
Figure 21. Différences entre les solides et les liquides vis-à-vis des pressions : les solides rigides transmettent les forces, les liquides transmettent les pressions.

a) En poussant le solide de droite avec une force f, celle-ci est transmise de l’autre côté ; par contre si, entre les deux faces d’un dispositif de même forme mais contenant  un liquide, on pousse avec la même force f sur le petit piston de surface s, on génère une pression p à l’intérieur de tout le liquide, d’où, au niveau du piston S (S> s) une force supérieure à f, proportionnelle à S : c’est le principe du vérin (ou cric) hydraulique illustré en b.

b) Principe du vérin (ou cric) hydraulique utilisé pour soulever un objet lourd : la force qu’il est possible d’exercer pour soulever un poids est proportionnelle au rapport des surfaces : F = f (S/s). Ainsi, si le rapport des surfaces est de 1 à 100, en appuyant sur le piston s avec une force de  20 « kilos » (on devrait dire de 200 N), on peut en principe soulever 2000 kilos. D’après Curie, 1961, et Kane et Sternheim, 1986, modifiés.

La masse d’un objet correspond à la quantité de matière qu’il contient. Elle se mesure avec une balance, en kilogrammes par exemple ; elle est indépendante du lieu. Le poids d’un objet dépend, lui, du lieu : sur la lune, on le sait, l’accélération de la pesanteur est bien inférieure à celle de la Terre et le poids d’une même masse y est donc moindre que sur la Terre. Une même masse n’a donc pas le même poids sur la Terre ou sur une autre planète. Le poids est une force ; il se mesure avec un dynamomètre^[16]. L’unité de poids est le Newton défini ci-dessus.  Poids et masse sont reliés par une grandeur physique fondamentale, « l’accélération de la pesanteur », g :

                                                                       Poids  = M x g                                                  équat. 10           

Poids = force exercée par la masse M (MLT^-2, newtons)
M = masse (M, kilogramme)
g  =  accélération de la pesanteur (LT^-2, ms^-2) = 9,81 ms^-2

L’accélération de la pesanteur, g, rend compte du fait qu’un corps de masse m, soumis à une accélération g, génère une force égale à son poids. De même l’équation 10 montre que le rapport du poids d’un corps sur sa masse est égal à l’accélération de la pesanteur. Autrement dit, une même masse peut correspondre à plusieurs poids selon la valeur de la gravité : ainsi un même objet « pèse moins lourd » sur la Lune que sur la Terre.

C’est par abus de langage que l’on parle de poids en kilos ou en grammes. On devrait dire « masse » de tant de kilogrammes ou de tant de grammes.

Dans la figure 21b la masse M du camion produit une force F dirigée vers le bas, égale au produit Mg :

                                                                       Poids = F = Mg                                                        équat.10’

A son tour cette force exerce sur le piston de section S une pression P, donnée par la relation 9 ci-dessus.

Application. Calculer la pression exercée par une personne de 65 kg sur le sol, quand elle est chaussée de chaussures habituelles avec une surface de semelle de 250 cm² en contact avec le sol, ou de patins à glace offrant une surface totale de 20 cm² (1 cm² = 1 x 10^-4m²).

La force verticale F qu’exerce un objet de masse m à la surface de la terre est donnée par la relation 10’  ci-dessus. Cette force F exercée par la personne est F = 65 x 9,81 = 6,4 x 10² N. Elle est la même quelles que soient les chaussures portées.

Les pressions exercées elles, diffèrent avec la surface :

- avec les chaussures normales : P1 = 6,4 x 10²/250 x 10^-4 = 25600 Pa (ou 0,25 atm)

- avec les patins à glace : P2 = 6,4 x 10²/ 20 x 0^-4 = 320000 Pa (ou 3,16 atm).

 

<Pression dans un gaz (fig. 22)

On peut enfermer une certaine quantité de gaz dans une enceinte. Pour une température donnée, ce gaz a une pression donnée (Cf.eq 6 : P=nRT/V), laquelle peut être déterminée à l’aide d’un manomètre. Si l’on dispose d’une pompe, on va pouvoir extraire du gaz de cette enceinte. Plus on extrait du gaz plus la pression de ce gaz baisse. Si l’on dispose d’une pompe à vide très puissante, on va pouvoir « faire le vide » c’est-à-dire en fait s’approcher d’une pression nulle laquelle ne pourrait être atteinte que s’il ne restait aucune molécule de gaz dans l’enceinte.  Cette pression nulle est par conséquent une limite de pression pour un gaz.

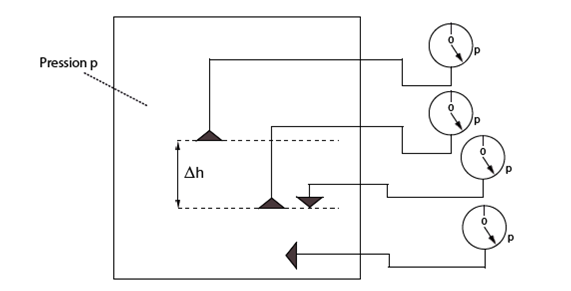
Figure 22. Mise en évidence de la  propriété d'un gaz vis à vis de la pression. Si dans une enceinte fermée, on place un capteur de pression, quelque soit son orientation et sa position dans le volume de l'enceinte, la pression qu'il mesure est toujours la même. Conclusion : dans  un volume fermé de gaz la pression est la même partout. Comparer avec la même expérience faite avec un liquide (Fig. 26).

La pression d’un gaz peut se mesurer à l’aide d’un manomètre très simple, reposant sur les deux propriétés des liquides vues précédemment : égalité de la pression sur un même plan horizontal et différence de pression proportionnelle à la hauteur séparant deux plans. Le principe de la mesure repose sur ces deux propriétés des liquides.

Le dispositif est le suivant (fig. 23) : un récipient qui contient un gaz dont on veut déterminer la pression P, est relié à un tube en « U » contenant un liquide de densité ρ connue. La branche de gauche est reliée au récipient, la branche de droite est ouverte à l’air libre : elle subit donc la pression atmosphérique. Calculons la pression dans chaque branche, en prenant le bas du tube en U comme référence. A l’équilibre les niveaux sont fixes et la pression est la même dans chaque branche.

En mesurant les hauteurs à partir du bas du tube en U et en appliquant la relation 11’ on a :

- branche de gauche : P_gauche= P + ρgh₁

- branche de droite : P_droit= P_atm + ρgh₂

A l’équilibre ces deux quantités sont égales donc P = P_atm + ρg(h₂- h₁) = P_atm + ρgh

La pression P mesurée (au-dessus de la pression atmosphérique) est donnée par la différence de hauteur d’eau h.

                         

                                       

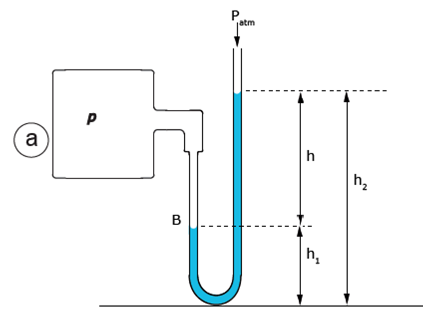
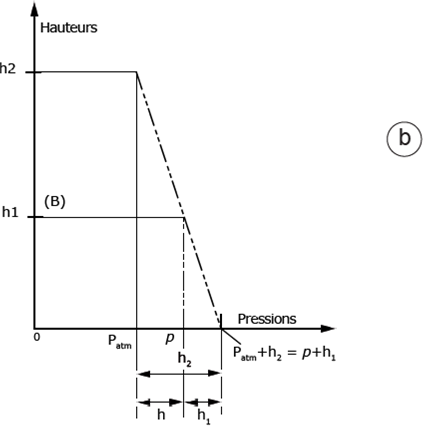
Figure 23. Principe de la mesure des pressions à l’aide d’un manomètre en U.
a) Le récipient qui  contient le gaz dont on veut déterminer la pression P est relié à un tube en U, contenant un liquide dont on connaît la densité. Si les pressions étaient égales dans chacune des deux branches du tube, le niveau du liquide serait le même dans les deux branches. Le fait qu’il soit plus haut dans la branche de droite indique que la pression P est supérieure à la pression atmosphérique d’une valeur (h) proportionnelle à la différence de niveau du liquide entre les deux branches.
b) Profils des pressions dans les deux branches à l’équilibre. D’après Kane et Sternheim, 1986, modifié.
Pour simplifier on a fait intervenir sur l’axe des pressions la hauteur h mais c’est en fait le poids de chaque colonne d’eau qui intervient

 

Application 1 (fig. 24). Supposons que l’on veuille établir une pression p’ de 1,5 atm dans un cylindre fermé par un piston et contenant un gaz de volume v, initialement à la pression atmosphérique p. La section du piston S est égale à 20 cm². Il faut donc comprimer le gaz. Quel poids (ou quelle masse M) doit-on poser sur le piston pour produire cette compression ?

La masse posée sur le piston doit être capable d’augmenter la pression de telle sorte que l’égalité ci-dessous soit satisfaite :

                                               p + p_masse = 1,5 atm = p’

p étant la pression initiale (atmosphérique) dans le cylindre et p_masse la pression supplémentaire à produire par la masse M.

On tire donc                             p_masse  = 1,5 – 1,0 = 0,5 atm ou 0,506 x 10⁵ Pa                                

La force (poids) F que doit exercer la masse à poser sur le piston doit être telle que F = p_masse x S

soit : 0,506 x 10⁵ Pa x 20 x 10^-4 m² =  101,3 newtons, soit 101,6/9.81 = 10,32 kg.

Il faut donc poser une masse d’environ 10 kg sur la face extérieure du piston pour maintenir une surpression de
0,5 atmosphères et faire que la pression passe de p à p’ = 1,5 atm.

                  

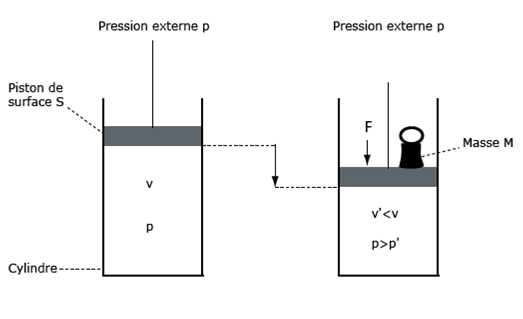
Figure 24. Une masse peut produire une pression. Si l’on veut augmenter la pression p dans le cylindre, on peut diminuer son volume (loi des gaz parfaits, § III.2), en enfonçant le piston qui le limite. Cette descente du piston peut être obtenue en posant une masse M sur le haut du piston. Cette masse a un poids : celui-ci exerce une force F, dirigée verticalement et vers le bas ; F s’exerce sur toute la surface du piston ; elle produit ainsi une pression qui va comprimer le volume de gaz et amener sa pression à une valeur supérieure p’.  L'expérience pourrait être faite avec un liquide et un piston hermétique, le résultat serait le même.

Application 2.  La mesure de la pression atmosphérique.

En 1643, Torricelli^[17], reprenant une idée de Galilée, remplit de mercure un tube de verre long de 1,30 m et renverse celui-ci dans une cuve à mercure (fig. 25). Il constate alors qu’une partie du mercure reste dans le tube et qu’un vide se forme à sa partie supérieure. Il a donc été le premier a réaliser ainsi un vide permanent. Après de longues observations, il conclut que les variations de la hauteur du mercure, d’un jour à l’autre, sont dues à des changements de la pression atmosphérique. C’est l’origine du baromètre à mercure (qui n’est qu’un manomètre particulier), pour la mesure des variations de la pression atmosphérique. La hauteur du mercure donne la mesure de cette pression 
(p = ρgh, équation11) :

                                    p = 0,76 m x 13600 kg m^-3 x 9,81 m s^-2 =  101396 Pa soit ≈ 1 atm

                                   

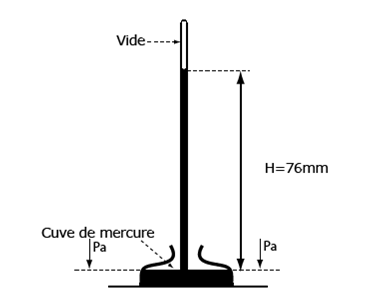
Figure 25. Tube de Torricelli servant à mesurer la pression atmosphérique.  Un tube fin en verre, d’environ 1m est rempli de mercure. Si on le renverse sur une petite cuve, elle aussi pleine de mercure, ouverte, et qu’on le dresse verticalement, une partie du mercure s’écoule et une autre reste dans le tube. Un espace vide se crée alors dans la partie supérieure. Dans un liquide à l’équilibre, la pression dans un plan  horizontal est la même. Donc à la surface du mercure de la cuve, que ce soit à l’aplomb du tube de verre ou à l’extérieur, la pression est la même. C‘est la pression atmosphérique, laquelle est ainsi mesurée par le poids qu’exerce la colonne de mercure sur la surface de la cuve à mercure. On aurait pu remplir le tube avec de l’eau mais pour exercer le  même poids qu’une colonne de mercure de 76 cm, la hauteur du tube devrait être de 10,3 m.

<Pressions dans un liquide

La pression dans un liquide (fig. 26) est analogue à la pression dans un gaz, mais il faut tenir compte de la grande différence de densité (ou de masse volumique), entre liquide et gaz. Si donc on refait l’expérience de la figure 22 en remplaçant le gaz par un liquide, on retrouve les résultats vus pour un gaz : la pression est la même dans un même plan et il existe  une différence des pression entre deux plans séparés par une certaine hauteur ; cependant pour un gaz, du fait de la valeur très faible de la masse volumique, la différence de pression entre deux niveaux est négligeable, sauf sur des hauteurs importantes^[18]. Le cas C de la figure 26 ne peut être transposé sans donner une précision de plus : les parois de l’enceinte où se trouve le gaz peuvent être rigides et ne pas transmettre la pression, mais la pression p s’exerce sur la surface libre du liquide et est transmise en tout point du liquide (page 29).

Concernant la pression, il existe une différence fondamentale entre les liquides et les gaz : alors que dans les gaz la pression est toujours  positive ou nulle, on peut trouver des pressions négatives dans les liquides. Comme on le verra, c’est même la situation de loin la plus commune dans le drpe.

Pressions positives

La figure 26 rappelle, à l’aide de trois observations simples faites avec un manomètre, les principales propriétés d’un liquide vis-à-vis de la pression. Le dispositif comporte un récipient plein d’eau et un manomètre précis dont le capteur peut être déplacé.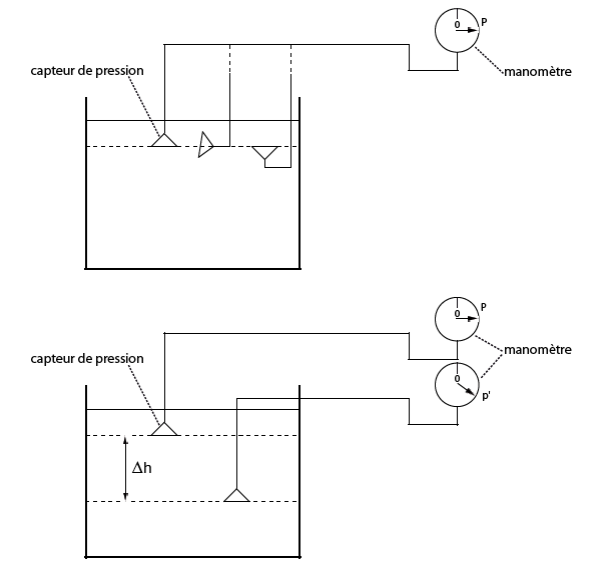

        

Figure 26. Mise en évidence des principales propriétés d’un liquide vis à vis de la pression. On dispose un capteur de pression relié à un manomètre pour mesurer la pression à différents emplacements dans le volume d’eau.
a). On déplace le capteur dans un même plan en le tournant dans toutes les positions possibles : la pression ne change pas. Elle s’exerce donc dans toutes les directions.
b) On dispose de deux capteurs que l’on place à deux niveaux différents dans l’eau : on constate que la pression est d’autant plus importante qu’on est loin de la surface d’une part, et que la différence de pression entre deux niveaux est proportionnelle à la différence de hauteur entre ces deux niveaux d’autre part.
c) On met le récipient plein d’eau dans un conteneur fermé dans lequel on monte la pression d’une valeur p au-dessus de la pression atmosphérique. On retrouve les résultats précédents mais les valeurs de pression sont toutes augmentées de la valeur p. Conclusion : les liquides comme les gaz transmettent les pressions.

La 1^ère observation (figure 26a) permet de conclure que la pression est uniforme dans un plan horizontal. La 2^ème observation (figure 26b),que la pression varie proportionnellement avec la profondeur où se trouve le manomètre par rapport à la surface du liquide. La troisième observation (figure 26c) illustre une autre propriété fondamentale des liquides définie par le théorème (ou principe) de Pascal^[19] : « Les liquides en équilibre transmettent les variations de pression auxquelles ils sont soumis ».

La pression en un plan situé à la distance h de la surface est donnée par le poids d’un cylindre de fluide ayant pour base l’unité de surface et pour hauteur la distance à la surface. Cet énoncé peut se généraliser à la pression séparant deux hauteurs à l’intérieur du liquide :

                                               P’- P = ∆hρg                                                                                               équat. 11

avec :

P’ : pression dans le plan situé à h’ de la surface (ML^-1T^-2, newtons)
P : pression dans le plan situé à h (h > h’) de la surface (idem)
∆h = différence de hauteur entre les deux plans = h- h’ (L, m)
ρ = masse volumique (densité) du liquide (ML^-3 ; eau : 1000kg m^-3)
g = accélération de la pesanteur (LT^-2, 9,81 m s^-2).

Si le liquide est celui d’un récipient à l’air libre, à une profondeur h, la pression à ce niveau h sera donnée par :      

                                               P_h= P_atm + ρgh                                                                                             équat. 11’

Application : calculer la pression P_h, à une profondeur de 100 m sous le niveau de la mer (on suppose que la densité de l’eau ne varie pas avec la profondeur, ce qui est vrai à quelques millièmes près) :

Il faut calculer ρgh :

ρgh = 1000 kg m^-3 x 9, 81 m s^-2 x 100 m = 9,81 x 10⁵ newtons par m² soit ≈ 10⁶ Pa ou encore environ 10 atmosphères (au-dessus de la pression atmosphérique puisque, à la surface de l’eau, la pression est déjà à 1 atm).

 

Pressions négatives (ou tensions) dans l’eau liquide

On a vu précédemment que, si l’on extrait le gaz contenu dans une enceinte, la pression restant dans l’enceinte sera d’autant plus proche de zéro que la pompe sera puissante. Cependant cette pression ne sera jamais négative : on a vu qu’elle résultait des chocs des molécules gazeuses sur les parois : s’il n’y a plus de molécules, la pression devient donc nulle. La valeur « zéro » est donc la valeur la plus basse qu’on puisse trouver chez un gaz.

Il n’en est pas de même avec un liquide et en particulier avec l’eau. L’eau peut être mise en « tension » et pas seulement en pression. Cette tension est une pression négative. Les pressions négatives qu’on peut obtenir dans un liquide sont fonction des contraintes mécaniques auxquelles celui-ci est soumis.

Bien que cette notion soit quelque peu dérangeante, elle est tout aussi réelle que la notion de pression positive. Elle a une importance capitale dans le domaine des relations entre les plantes et l'eau puisque l’eau dans les plantes et en particulier celle de la sève xylémienne, est la plupart du temps en état de tension. On la retrouvera donc tout au long de ce document. Elle sera en particulier étudiée au chapitre I.3 avec les autres phénomènes physiques (capillarité, cavitation...) auxquels elle est liée. Ce paragraphe n’est donc là que pour aider le lecteur à accepter l’existence de ces pressions négatives en lui présentant un dispositif simple capable de les générer : un tube capillaire très fin placé au-dessus d’un plan d’eau (fig. 27). Une étude plus approfondie des phénomènes capillaires est l’objet du chapitre I.3.

Voyons comment ces pressions négatives apparaissent (cf. fig. 27).

Supposons donc que l’on dispose de deux tubes capillaires en verre, ouverts aux deux bouts et chacun d’un diamètre différent. Leur extrémité inférieure plonge dans l’eau.  On constate que la hauteur d’eau dans chaque capillaire (on en a représenté deux seulement dans la figure) est d’autant plus haute que le capillaire est fin (voir chap I.3).

Par application de ce qui a été dit plus haut on sait qu’au niveau de la surface de l’eau du récipient, la pression est la même dans le capillaire et à l’extérieur (sinon il y aurait un échange d’eau). Cette pression est connue : c’est la pression atmosphérique. Or dans le tube capillaire, il y a une certaine hauteur d’eau qui pèse en plus. Pour qu’un équilibre se réalise néanmoins dans ces conditions (même pression à la base du capillaire et à la surface du liquide extérieur), il faut qu’il existe une force s’exerçant sur la colonne d’eau du capillaire, égale au poids de cette colonne d’eau mais dirigée vers le haut. La capillarité est précisément le phénomène physique à l’origine de cette force qui s’exerce au niveau de l’interface paroi du capillaire-eau, et génère cet effet de traction vers le haut sur la colonne d’eau. Plus le diamètre du capillaire est fin, plus les forces capillaires sont grandes et plus la colonne d’eau nécessaire pour les contrebalancer doit être haute. 

 

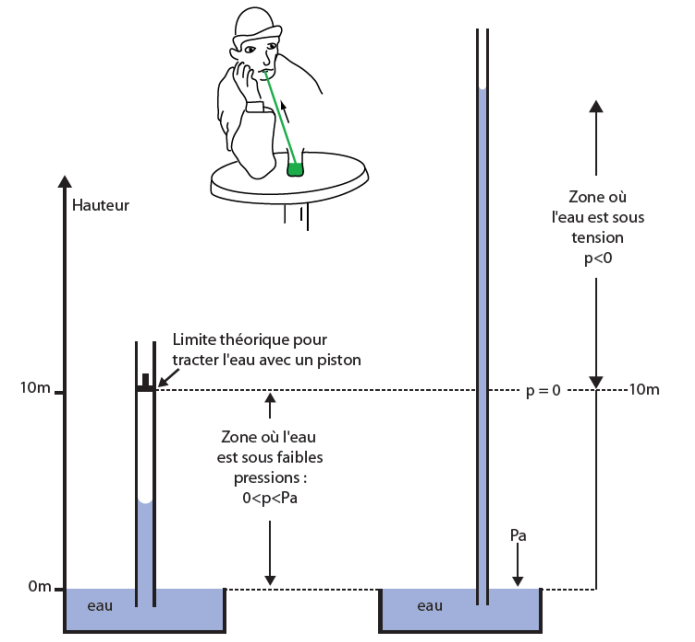
Figure 27. Pressions négatives ou tensions.
a) Quand on aspire avec une pipette un liquide placé dans un récipient ouvert à l’air libre, on exerce sur lui une force opposée à son poids (flèche). Du coup une différence de pression se crée entre la pression de l’eau dans la pipette et la pression dans l’eau dans le récipient laquelle est légèrement plus haute (c'est la pression atmosphérique). Cette différence de pression permet que s’établisse un courant d’eau de l’extérieur vers la pipette. D’après Tardy, 2007.
b et c).Si on utilise un capillaire très fin (plus fin que la pipette dont il vient d'être question) c'est un phénomène d'attraction (appelée tension superficielle) qui va jouer le rôle du buveur. Cette attraction dépend du diamètre du capillaire : plus celui-ci est fin plus l'attraction, dirigée vers le haut est importante. D'un côté il y a le poids de la colonne d'eau, dirigé vers le bas et qui augmente avec sa hauteur, d'autre part l'attraction de cette colonne, fixe pour un diamètre donné. Pour une certaine hauteur ces deux forces vont s'annuler : la colonne sera donc à pression nulle. Pour des diamètres plus fins, la résultante sera une pression négative ou tension. C'est ce qui a lieu dans les très fins capillaires que constituent les vaisseaux des plantes. Voir aussi chap. I.3.

Deux situations peuvent alors se produire :

- les forces capillaires sont suffisantes pour élever une colonne d’eau correspondant à la pression atmosphérique (soit 10 mètres environ). La résultante des forces exercées à la base de cette colonne est alors nulle (pression atmosphérique moins le poids d’une colonne d’eau équivalent à cette pression atmosphérique).

- les forces capillaires sont plus importantes et capables de « tirer » une colonne d’eau supérieure à celle équivalente à la pression atmosphérique : la pression dans la colonne devient alors négative ; on dit que la colonne d’eau est sous tension c’est-à-dire en pression négative.   

La pression au sommet d’une colonne d’eau de hauteur h est donnée par la même équation 11 précédente, à cette différence que le niveau de la colonne est au dessus du plan de référence et non plus au-dessous. Au niveau du ménisque, en haut de la colonne la pression P_c est donc donnée par l’expression ci-dessous :

                                                  P_cap = P_atm - ρgh                                                                               équat. 11bis

P_cap = pression au niveau du ménisque en haut de la colonne d’eau

P_atm = pression atmosphérique

ρgh  = pression due à la colonne d’eau de hauteur h j

On retrouve avec cette équation ce qui vient d’être dit précédemment :

- si la hauteur h d’eau correspond à la pression atmosphérique, les deux termes de l’équation ci-dessus s’annulent et la pression au sommet de la colonne d’eau, P_cap est nulle,

- si cette hauteur d’eau h dans le capillaire est supérieure à celle correspondant à la pression atmosphérique, le terme rgh est supérieur à P_atm et P_cap  est négatif : la colonne est sous tension.

 

L’état solide : la glace.

Comme les liquides et les gaz, les solides possèdent un volume défini mais, contrairement à eux, ce volume a une forme qui lui est propre (cf. tab. 1). C’est dans cet état que les molécules sont les plus rapprochées les unes des autres, les plus liées et les plus ordonnées, et que les mouvements moléculaires sont les plus limités. Du fait de cette disposition moléculaire les solides sont incompressibles^[20].

De même que le gaz parfait est caractérisé par un désordre « parfait », c’est-à-dire complètement aléatoire, de la répartition de ses molécules dans l’espace, le solide parfait est un solide dans lequel atomes ou molécules sont répartis dans un ordre parfaitement régulier. Il possède une structure de cristal parfait. Les solides réels présentent des écarts plus ou moins grands avec ce modèle de cristal. Ainsi, l’incompressibilité d’un solide est relative : si les forces deviennent suffisamment importantes, celui-ci se déforme. Une fois les forces retirées, s’il retrouve sa forme initiale on dit alors qu’il est élastique. Si la déformation est permanente on dit que la limite d’élasticité a été franchie et on parle alors de plasticité. Nous verrons (chap. II.3) que les parois des cellules végétales sont des solides à la fois élastiques et plastiques et que ces propriétés interviennent dans les variations de l’état d’hydratation des cellules.

L’état solide de l’eau se présente sous des formes très différentes (neige, givre, verglas, grésil, grêlons, glaces...) correspondant toutes à des assemblages extrêmement divers de cristaux de glace hexagonaux, dont la formation comme l’évolution font intervenir un grand nombre de processus physiques complexes. L’arrangement spatial des molécules d’eau est celui d’un cristal, les atomes formant un réseau géométrique très précis, mais dont la disposition atomique varie considérablement^[21] comme on peut s’en rendre compte à travers l’extrême variabilité de la forme des  cristaux, laquelle cependant est toujours hexagonale (fig. 28b)^[22] C’est la raison pour laquelle il faudrait parler de « glaces » et non de « glace ». Selon les conditions de température (au-dessous de zéro bien sûr) et de pression (pressions différentes entre couches de surface ou profondes dans un glacier par exemple ou bien hautes pressions produites en laboratoire) on rencontrera des glaces à la structure et aux propriétés physico-chimiques très différentes. La glace la plus commune, dite « glace I » est construite en forme de réseau cristallin globalement hexagonal (fig. 4 et 28a).

La structure de la glace, contrairement à d’autres solides est ouverte : les molécules d’eau y sont relativement mobiles, les charges électriques peuvent s’y déplacer (mais sa conductivité reste extrêmement faible en l’absence d’impuretés) et on y trouve des défauts cristallins de type ionique c’est à dire formés par un proton hydraté (H₃O⁺) ou un ion hydroxyde (OH^-). Ces défauts augmentent avec la présence d’inclusions, de nature chimique et physique très variable, qui peuvent modifier profondément certaines des propriétés de la glace.  Ainsi par exemple la résistivité^[23] électrique de la glace parfaitement pure est de 100 Ω.m alors que celle d’un glacier, peut être de l’ordre de 0,01 Ω.m ! Lorsque la glace fond, les trous qui se forment sont remplis par des molécules d’eau liquide interstitielle.

    

 

           

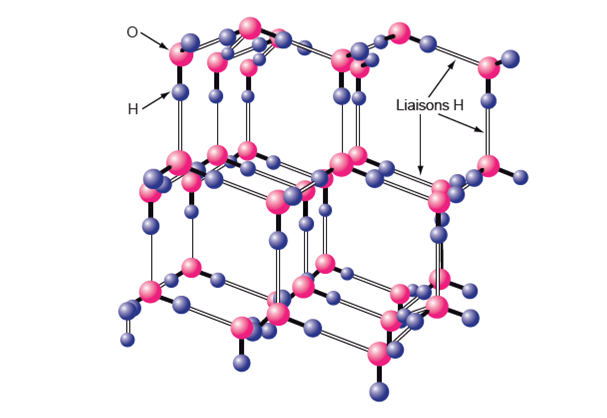
Figure 28. Structure de la glace ordinaire et formes de cristaux.
a) La glace forme des cristaux. Dans un cristal de glace, les molécules d’eau sont disposées selon des plans réguliers. Dans un même plan chaque molécule est entourée de trois autres (voir la figure 4c) ; cette disposition est celle d’un réseau hexagonal. La glace est cependant une structure « ouverte » dans laquelle les molécules peuvent bouger autour de  positions d’équilibre.
b) Exemples de structures de cristaux parmi les dizaines ou centaines répertoriées. On voit qu’une même disposition au niveau moléculaire peut générer des cristaux extrêmement différents, (quoique tous de type hexagonal), du fait de la grande  variabilité des conditions de leur formation.Source : http://www.di.ens.fr/~granboul/enseignement/formes/cristauxneige/

On a vu précédemment que la structure de la glace était gouvernée par l’agencement des atomes d’oxygène et des liaisons H. Ces liaisons y sont beaucoup plus nombreuses que dans l’eau liquide. Elles provoquent un éloignement des atomes. Il en résulte que la glace est moins dense que l’eau liquide (fig. 29) et flotte sur celle-ci. L’augmentation de volume lors de la cristallisation met en jeu des forces considérables susceptibles de faire éclater une bouteille de  verre mais aussi des pierres ou du bois. De même, si l’eau des cellules d’une plante se change en glace, celles-ci éclatent (voir chap.III.5).

 

             

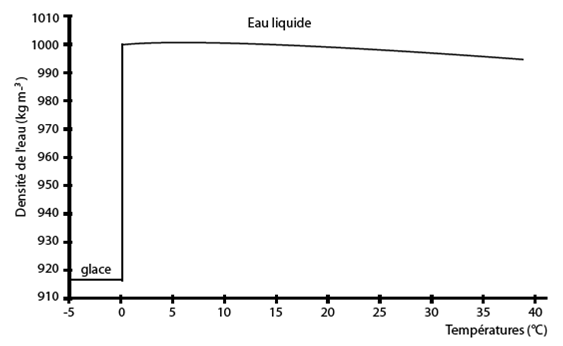
Figure 29. Brusque variation de la densité de l’eau autour de 0° C : en passant de 0°C à -5°C, elle chute de 999 KG masse^-3 à environ 917 kg m^-3 soit environ une baisse de 8%. Voir figure 17. D’après Denny 1993.

Une autre conséquence de cette structure particulière est que l’application d’une forte pression (à température constante) a pour effet de « casser » des liaisons H, ce qui conduit à la fonte de la glace. On peut s’en rendre compte de façon simple en attachant deux poids aux extrémités d’un fil fin placé sur un glaçon. La pression exercée par le fil peut être suffisante et induire une fusion de la glace. L’eau peut se solidifier à nouveau après le passage du fil qui peut ainsi traverser le glaçon sans le casser.

Un autre exemple qui se rapproche du précédent est celui du patin à glace. Comme on l’a vu ci-dessus du fait de sa finesse, la lame du patin exerce une forte pression sur la couche de glace superficielle, qui se liquéfie. Le très fin film d’eau qui se produit alors agit comme un lubrifiant améliorant la glisse.

De même encore, ce passage de la phase solide à la phase liquide sous l’effet de fortes pressions (et à températures négatives) explique, en partie, le fait qu’à la surface inférieure des glaciers, du fait de la pression considérable engendrée par l’épaisseur du glacier, il existe souvent de l’eau en phase liquide. Cependant si la température est suffisamment basse et que la pression diminue, l’eau gèle à nouveau.

La glace est aussi très légèrement élastique c’est-à-dire capable de variations réversibles de sa forme ; ces déformations élastiques peuvent, sous certaines conditions, se maintenir dans le temps et devenir ainsi des déformations permanentes dites plastiques. Un tel comportement à la fois élastique et plastique se retrouvera dans les parois pectocellulosiques des parois végétales (chap. II.3).

A la pression atmosphérique les gaz sont peu solubles dans la glace : de l’ordre de 0,1 cm³ par gramme de glace ; c’est bien moins que dans l’eau liquide^[24] (cf. tab 3). Cette baisse de solubilité des gaz est un phénomène capital dans l’embolie hivernale des arbres. En effet la congélation de la sève expulse les gaz dissous qu’elle contient. Ceux-ci sont bloqués dans les éléments conducteurs et forment alors un « bouchon » de gaz qui devra être résorbé pour que la sève puisse à nouveau passer.

Nous venons de voir les trois états de l’eau et leurs principales propriétés ; nous allons maintenant traiter de différents aspects du passage d’un état à l’autre.