Compléments

C1. Solutions réelles concentrées : activité de l’eau

Ce court paragraphe a pour objet de rappeler au lecteur que les solutions réelles peuvent avoir un comportement différent de celui des solutions idéales. Limitons nous au cas de l’eau et rappelons quelques définitions.

·        Solvant pur : le solvant pur est caractérisé par ses relations P,T. Par exemple pour l’eau il va s’agir des courbes traduisant les équilibres liquide-glace-vapeur en fonction des conditions de T et P. (diagramme des phases)

·        Solution idéale : d’un point de vue théorique, une solution est dite idéale si les interactions entre molécules de cette solution, toutes espèces confondues, ne sont pas altérées du fait de la présence des autres espèces. Autrement dit, les molécules des différentes espèces s’attirent ou se repoussent entre elles de la même façon que les molécules de chaque espèce à l’état pur s’attirent ou se repoussent entre elles (Wikipedia). D’un point de vue plus pratique, la solution idéale obéit aux lois de Raoult (vues dans ce chapitre) c’est à dire que, entre autres choses, la pression de vapeur en équilibre avec la solution est proportionnelle à la fraction molaire N_i de l’eau dans le mélange. L’abaissement cryoscopique et l’élévation de la température d’ébullition sont proportionnels à la fraction molaire du soluté. D’une façon générale, la présence de solutés n’a qu’un effet de dilution sur le solvant.

·        Solutions réelles : les solutions réelles peuvent être regroupées, quelque peu arbitrairement, en trois grands types de solutions liquides non idéales :

- i) les solutions concentrées mais dans lesquelles le soluté reste sous forme moléculaire. Les unes contiennent des molécules de petites dimensions (ex. : glucose) et sont transparentes et stables. Les autres contiennent des macromolécules (ex. : des protéines, des polymères) qui leur confèrent des propriétés cinétiques et électriques particulières. Elles sont en général translucides et instables. On parle de solutions colloïdales, leurs solutés s’appelant des colloïdes ;

-  ii) les solutions dont le ou les solutés sont sous forme d’ions (solutions ioniques) et qui conduisent le courant électrique ;

- iii) les solutions qui sont à la fois concentrées et ionisées.

Leur étude est hors de l’objet et du niveau de ce site.  De plus, à quelques exceptions près, ces cas plus ou moins complexes ne jouent pas un rôle majeur dans les échanges d’eau. Par contre leurs effets sur les transports moléculaires et ioniques sont souvent déterminants. Il est donc indispensable de les connaître lorsqu’on s’intéresse à la physiologie de l’absorption minérale des plantes en particulier. On reviendra cependant sur ce point à propos de l’eau au niveau cellulaire (chapitre II.1).

Terminons en donnant un exemple de la façon dont on peut étendre, pour toutes ces solutions non idéales, la notion de concentration définie plus haut pour les solutions idéales.

Pour résoudre la question, on remplace la variable « fraction molaire vraie » du solvant par une autre, appelée « activité » tout en conservant les lois des solutions idéales. L’activité a_eau  de l’eau ainsi introduite est une sorte de concentration corrigée définie comme suit :

                                                                                                  équat. 27

avec :

a_eau  = activité de l’eau (sans dimension)

g_eau = coefficient d’activité (sans dimensions, < 1 ou >1 selon les cas) 

N_eau= fraction molaire de l’eau (nombre de moles d’eau sur le nombre total de moles dans la solution ; nombre sans dimensions)

Pour l’eau, la valeur de l’activité a_eau  est donnée très simplement par :

                  <1                                                                         équat. 28

p_solution  = pression de vapeur d’eau en équilibre avec la solution (Pa)

      = pression de vapeur saturante de l’eau pure à la même température (Pa)

On peut donc déterminer a_eau, en mesurant la pression de vapeur p_solution en équilibre avec la solution. La pression osmotique de la solution pourra également être calculée par :

             (Pa)                                                                   équat. 29

On retrouve bien l’équation 8 dans laquelle l’activité a remplacé la concentration. La présence de solutés tend à diminuer l’activité du solvant eau, alors que l’activité du soluté augmente avec sa concentration. La pression osmotique et l’activité a_eau varient donc en sens contraire.

C2. Solutions ionisées, macromolécules, équilibre de Donnan.

La diffusion des solutés entre deux compartiments séparés par une membrane poreuse à l’eau et aux petites molécules ou ions de soluté, est provoquée par une différence de concentration entre ces compartiments ; l’équilibre intervient et le flux net de solutés cesse lorsque les concentrations sont les mêmes de part et d’autre de la membrane. Cette conclusion n’est plus vraie si l’un des compartiments contient, en plus des ions et petites molécules, de grosses molécules chargées électriquement et pour lesquelles la membrane est infranchissable ; l’équilibre ne correspond plus alors à l’égalité des concentrations dans les deux compartiments.

Les processus de Donnan s’inscrivent dans ce cadre. Ils « traduisent les interactions entre petits ions mobiles et charges électriques immobiles donc non diffusibles. On les rencontre dans la quasi-totalité des sous-structures cellulaires » (Thellier et Ripoll, 1992). Ainsi ces charges non-diffusibles correspondent à la présence, dans les parois et les membranes par exemple, de molécules plus ou moins volumineuses, piégées dans ces structures. Ces molécules portent plusieurs charges électriques (d’où leur nom de polyions ou polyélectrolytes). Les résines « échangeuses d’ions » utilisées en particulier pour purifier l’eau, constituent un exemple de polyélectrolytes fixés qui, piégés dans une structure membraneuse artificielle, ne peuvent la traverser, quels que soient leur signe et le nombre de charges qu’ils portent (monovalent, polyvalent). Autre exemple : le cytoplasme cellulaire qui contient des anions formés par les  groupes carboxylés des protéines ou par des polymères comme le RNA et le DNA. Tous ces édifices moléculaires sont chargés électriquement et ne traversent pas la membrane. Les régions contenant ces charges immobiles sont appelées phases (ou espaces) de Donnan.

L’équilibre de Donnan est donc un équilibre particulier d’ions qui s’établit entre un compartiment contenant des électrolytes piégés et un autre compartiment contenant des ions « libres » traversant la membrane. À l’équilibre (flux net d’ions nul)  les concentrations en ions ne seront pas les mêmes dans les deux compartiments. La présence d’une phase de Donnan a au moins deux conséquences sur la répartition des ions : i) la concentration totale dans le compartiment contenant les polyions est plus faible que dans le compartiment ne contenant que les ions mobiles ; ii) à l’équilibre, quand le flux d’ions est nul, il existe une différence de potentiel électrique entre les deux compartiments : c’est le potentiel de Donnan, qui est caractéristique des cellules vivantes. Il résulte du fait que les cations et les anions ne sont plus également répartis au niveau de la membrane. On trouvera dans Thellier et Ripoll (1992), Atkins (2000) des compléments expérimentaux et théoriques sur ces phénomènes de Donnan.

C3. Composantes de pression et de gravitation du Y . Cas d’un grand arbre en équilibre hydrique avec un sol saturé en eau.

On va supposer (fig.18) que les seules composantes du  de cet arbre sont  la composante hydrostatique et  la composante gravitationnelle. Le niveau de référence est la surface du sol et ce sol est saturé en eau sur 5m de profondeur (dans l’horizon où se trouvent les racines). Supposons cet arbre en équilibre avec le sol saturé ; cela signifie que sur toute sa hauteur, le potentiel hydrique vaut

Cette situation n’existe sans doute pas exactement dans les conditions naturelles mais on peut penser que les séquoias de la côte ouest californienne par exemple, en automne lors d’un épisode de brouillard, ou les arbres de certaines forêts humides sont soumis à des conditions très proches de ce cas théorique.

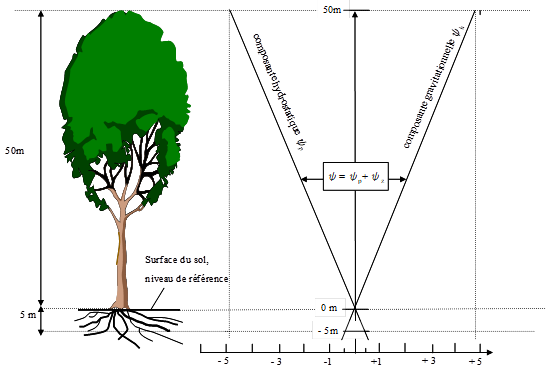
Figure 18. Profil théorique vertical des composantes hydrostatique et gravitationnelle du potentiel hydrique. Cas d’un arbre de 50 m de haut en situation d’équilibre avec un sol saturé sur 5m de profondeur. Le niveau de référence du potentiel est la surface du sol. On suppose qu’à chaque niveau, le potentiel hydrique ψ n’a que deux composantes, ψ_p et ψ_z (pas de composantes de turgescence et osmotique) et que le système est en équilibre avec le potentiel de l’eau d’un sol à saturation donc avec un ψ_sol = 0.

Examinons le profil de pression. À la surface du sol saturé l’eau est à la pression atmosphérique et les deux composantes  et  sont nulles. Au-dessus de ce plan, la pression diminue, tout comme elle diminue à l’intérieur d’un tube renversé sur un plan d’eau, quand on s’élève au dessus de la surface ou encore dans les pores de la frange capillaire qui surmonte une nappe dans un sol. Il en va de même pour l’eau qui se trouve à l’intérieur des tissus de l’arbre, en continuité hydraulique avec l’eau du sol. A l’altitude z la pression vaut . À 50 m par exemple elle vaut (-1,013 10⁵ Pa/ 10,35) x 50 = - 4,89 10⁵ Pa (environ -5 bars). Quant à la composante gravimétrique, Y_z = rgz, elle varie en sens contraire, de sorte qu’à tout niveau z on vérifie bien , ce qui est la condition d’équilibre hydrique entre l’arbre et le sol. On verra au chapitre II.8 comment ce profil « hydrostatique » est modifié quand l’arbre est traversé par un flux de transpiration.

C.4. Petite histoire de la notion de potentiel hydrique.

Pendant longtemps les différents spécialistes, physiciens du sol, physiologistes, agronomes s’intéressant aux flux d’eau dans le sol, dans la plante ou entre les  cultures et l’atmosphère, ont  travaillé de façon assez indépendante. Chacun dans sa discipline a donc développé, pour caractériser ces flux et ces états de l’eau, des lois plus ou moins empiriques, associant des grandeurs physiques spécifiques, exprimées en unités particulières : les physiciens du sol parlaient de « hauteur capillaire, » les physiologistes de « pression osmotique », de « déficit de pression de diffusion », ou de « pression de succion » ; les agronomes et les micrométéorologistes qui étudiaient les flux de vapeur entre les feuilles et l’atmosphère, utilisaient quant à eux les différences de concentration de vapeur d’eau. Lors du congrès international tenu en 1959 à Madrid, sur les « Échanges hydriques des plantes en milieu aride ou semi-aride » les discussions ont montré :

- que la description des états de l’eau, notamment dans le sol, relevait de la thermodynamique et, en particulier, qu’elle pouvait se faire à l’aide de variables comme l’enthalpie libre (ou énergie de Gibbs, qui caractérise l’état d’un système, faisant intervenir son énergie interne et les relations entre ce système et le milieu extérieur) et le potentiel chimique.

- qu’en conséquence, les multiples termes utilisés jusque-là par les physiologistes, les physiciens du sol, les agronomes, sources de difficultés et de confusion, pouvaient être avantageusement remplacés par une grandeur physique unique, valable pour les états liquide et gazeux de l’eau. Le potentiel chimique a d’abord été retenu, mais pour rester proche des biologistes on a préféré « inventer » une autre variable s’exprimant en pression : c’est ainsi qu’a été créé le potentiel hydrique, lequel offrait une terminologie unifiée, basée sur un fondement physique solide, pour caractériser l’état de l’eau dans le sol, dans un tissu végétal ou dans l’air. 

Dès les années 60, S.A. Taylor, professeur d’agronomie à l’université de Logan (Utah, USA) et R.O. Slatyer, chercheur au CSIRO à Canberra (Australie) sont chargés d’élaborer des propositions pour cette terminologie unifiée (Taylor et Slatyer, 1960a, Slatyer et Taylor, 1960b). Dainty (1963) proposera de rapporter le potentiel hydrique non pas à l’unité de masse mais à l’unité de volume, précisément pour pouvoir convertir facilement les concepts de pression osmotique et de pression de turgescence en potentiel hydrique.

Après avoir développé la base théorique justifiant le choix du potentiel hydrique comme variable la plus adéquate, ces auteurs en recommandent l’usage comme grandeur unique pour exprimer les flux dans le sol et dans la plante. Il est décidé que le symbole de cette variable « potentiel hydrique », sera la lettre grecque. Leurs propositions vont être progressivement acceptées quasiment unanimement. L’ouvrage fondateur de Slatyer, « Plant water relationships » paru en 1963, qui s’impose tout de suite comme une référence, fera beaucoup pour en répandre l’utilisation.

Parallèlement à ce travail, les agronomes, physiciens du sol, physiologistes, etc., ont multiplié les expérimentations pour essayer d’établir des lois susceptibles de décrire les transferts d’eau dans chacun des milieux considérés. La conduction de la chaleur dans les solides homogènes ainsi que la diffusion moléculaire en milieu gazeux ou liquide, phénomènes déjà largement étudiés et mis en équations par les physiciens au 19^ème siècle ont servi de modèles pour aborder l’étude des transferts de l’eau dans les milieux poreux complexes plus ou moins hétérogènes.

Les travaux de ces physiciens ont inspiré les approches analogiques modernes du CSPA et du DRPe dont nous avons tenté de rendre compte ici. Jack Dainty en particulier a exploré l’utilisation de la notion de potentiel hydrique et de ses gradients pour décrire les échanges d’eau inter et intracellulaires, ce qui ne va pas sans poser des questions fondamentales quant à la signification même de la notion de potentiel hydrique à d’aussi petites échelles. On peut dire que certaines de ces questions sont encore à l’ordre du jour.