Les transferts d’eau transmembranaires

Les membranes cellulaires sont très perméables à l’eau

Alors que la cellule végétale est entourée d’une paroi pectocellulosique rigide, c’est bien la membrane plasmique (le plasmalemme) qui « contient » l’eau intracellulaire et son contenu. Elle délimite le compartiment intracellulaire. Par ailleurs, la cellule végétale mature contient une vacuole, qui constitue une grande partie du volume cellulaire (voir Fig. 1). La vacuole est entourée elle aussi d’une membrane, le tonoplaste. Ces membranes sont constituées d’une bicouche phospholipidique (cf. Fig. 4), et les expériences de plasmolyse (par bain dans des solutions hypertoniques) montrent qu’elles sont très perméables à l’eau.

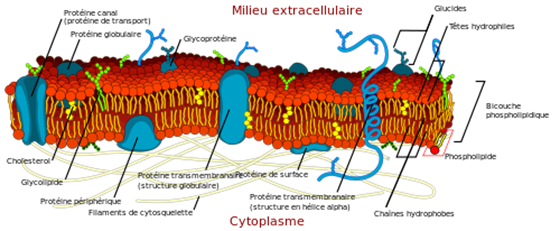
Figure 4.  Schéma d’une membrane plasmique. (source https://fr.wikipedia.org/wiki/Membrane_%28biologie%29)

L’eau étant une petite molécule non chargée électriquement, on n’a pas su pendant très longtemps si ces molécules traversaient les membranes en passant par diffusion à travers les éléments de la bicouche lipidique ou bien si elles passaient à travers des pores. Dans ce dernier cas, on imaginait des interactions entre solutés et molécules d’eau. Certaines études suggéraient que le transfert par diffusion était insuffisant pour expliquer les vitesses de transport de l’eau mesurées, mais aucun élément d’analyse microscopique ne mettait en évidence des pores. En 1992, des canaux transmembranaires permettant le passage de l’eau, dits « aquaporines », ont été découverts, d’abord dans des érythrocytes humains, puis très rapidement dans les membranes des cellules végétales et il a rapidement été montré que les aquaporines étaient responsables de la grande perméabilité à l’eau des membranes (cf. paragraphe ci-après).

Lois thermodynamiques régissant les flux d’eau transmembranaires

Le transport de l’eau à travers une membrane répond aux lois de la thermodynamique irréversible. Le flux d’un composant dépend de toutes les forces agissant sur tous les composants mobiles du système. Une des conséquences est que, eau et solutés étant et interagissant dans le même système, flux d’eau et flux de solutés sont inévitablement couplés.

Dans le cas d’un flux d’eau faible, le flux d’eau à travers une membrane perméable à l’eau et aux solutés est donné par :

                              J_v= L_p (DP – s DP)                                                                            (éq. 7)

Plus précisément, si on considère une solution où coexistent différents solutés imperméables (imp) et différents solutés perméables (p), on aura :

                             J_v= L_p (DP – DP_imp - Ss_pDP_p)                                                          (éq. 8)

où J_v est le flux d’eau (m³ m^-2 s^-1), DP et DP sont les différences de pression hydrostatique et de pression osmotique de part et d’autre de la membrane, c’est-à-dire entre l’intérieur et l’extérieur de la cellule, Lp est la conductivité hydraulique membranaire (m s^-1 MPa^-1) et s est le coefficient de réflectivité membranaire (sans unité).

Ainsi, la force déplaçant l’eau de part et d’autre de la membrane est le gradient de potentiel chimique de l’eau entre les deux compartiments. Lp et s affectent fortement le flux d’eau à travers la membrane.

Le coefficient de réflectivité membranaire s mesure la déviation du modèle de cellule considéré par rapport à un modèle présentant un comportement parfaitement hémiperméable. En général, les coefficients de réflectivité membranaire des différents solutés présents dans une cellule (sels, sucres et métabolites, …) sont très proches de 1 et la force d’attraction de l’eau à travers une membrane est bien approximée par la différence de potentiel hydrique. Le flux d’eau est ainsi purement proportionnel au gradient de potentiel hydrique.

                             J_v= L_p (DY)                                                                                        (éq. 9)

Cette relation détermine la dynamique des échanges d’eau d’une cellule avec son environnement. Supposons une cellule de volume V et de surface A, de paramètres hydriques P_ini et P_ini, en équilibre hydrique avec son environnement dont le potentiel est Y^ext, avec Y^ext = -P^ext (la pression extérieure à la cellule est nulle, c’est-à-dire qu’elle est égale à la pression atmosphérique).

Supposons qu’au temps t, la pression osmotique du milieu passe de P^ext à (P^ext + DP^ext). Ce changement de potentiel hydrique de l’environnement rompt l’équilibre hydrique et va générer un flux d’eau, accompagné de changements du volume cellulaire et de la pression de turgescence. Le flux d’eau entrant dans la cellule est donné par l’équation :                                                   

                                                              (éq. 10)

Où P(t) et P(t) sont la pression de turgescence et la pression osmotique de la cellule au cours du temps. Cette équation peut être intégrée pour obtenir P(t), V(t) et P(t).

Si la variation DP^ext est faible, la variation de turgescence est faible, les variations DP, DP, et DV sont faibles et on peut également considérer que A , e et Lp sont constants.

Si la membrane est parfaitement hémiperméable, le nombre de molécules de solutés est constant et :

                         P V = P_ini V_ini = constante

Ainsi :                   (DV étant faible, V≈V_ini)

Selon l’équation (6) :

Ansi :

Et ainsi, dans l’équation 10 :

Sachant que P_ini - P_ini = -P^ext (équilibre des potentiels hydriques au départ) : P^ext - P_ini= -P_ini :

Si on considère que P = P_ini à t=0 et que P = P_fin pour un temps infini, l’intégration de cette dernière équation donne :

                                                                (éq. 11)

Cette équation 11 décrit une relaxation de pression induite par un changement de pression osmotique (et donc de potentiel hydrique) du milieu extérieur (Fig. 5). Elle est vérifiée aussi pour une perturbation de l’équilibre hydrique suite un changement de la pression de turgescence de la cellule. La dynamique de changement de pression de la cellule est de type exponentiel avec une constante de temps inversement proportionnelle à la conductivité hydraulique de la membrane.

Le taux de variation k_w est donné par :

                                         (éq. 12)

où T^w est la constante de temps et T^w_1/2 est la demi-vie du processus.

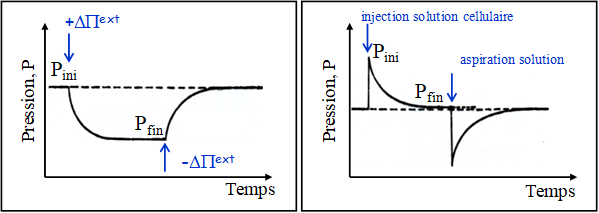
Figure 5. Dynamique de changement de pression de turgescence cellulaire liée à un flux d’eau (entrant ou sortant) induit par une perturbation du potentiel osmotique extérieur ou de la pression de turgescence cellulaire.

A l’aide d’une sonde à pression cellulaire (décrite dans le § II.1.6), on peut mettre en évidence cette dynamique de changement de pression au sein de la cellule. A t=0, l’injection d’un petit volume de solution dans la cellule induit une augmentation de pression, rompant l’équilibre hydrique de la cellule avec le milieu extérieur. L’eau va sortir de la cellule, ramenant progressivement celle-ci à l’équilibre hydrique avec son milieu. T^w_1/2 et Lp étant inversement proportionnels, un temps de demi-vie court (voir Fig. 6) indique une forte conductivité hydraulique membranaire, c’est-à dire un retour à l’équilibre rapide.

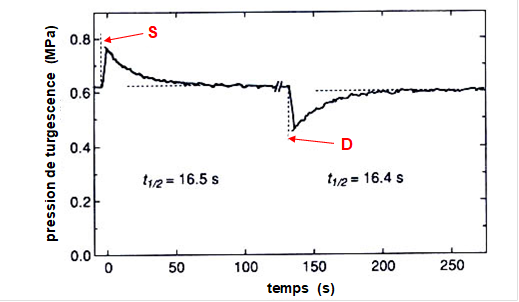
Figure 6.  Relaxation de pression d’une cellule végétale de Tradescantia virginiana suite à une surpression (S) ou une dépression (D). t_1/2 correspond au temps de demi-vie de la relaxation (d’après Tyerman and Steudle, 1982).

Mesure de Lp

Une technique basique pour quantifier la perméabilité du plasmalemme est l’induction de la plasmolyse par bain dans une solution hypertonique[4]. Suivie sous microscope, la vitesse de gonflement - dégonflement permet de calculer la conductivité hydraulique membranaire. Cependant cette technique est imparfaite, des phénomènes de couches limites altèrent la qualité de l’estimation de Lp.

La technique de sonde à pression cellulaire se démarque de cet inconvénient et permet d’accéder aux composantes du potentiel hydrique cellulaire (P et P) mais aussi au module d’élasticité cellulaire e et à la conductivité hydraulique membranaire Lp.

Comme nous l’avons vu ci-dessus, le suivi de la relaxation de pression suite à une perturbation de l’équilibre hydrique entre la cellule et le milieu extérieur dépend de Lp. Ainsi, d’après l’équation (12) :

                                                                         (éq. 13)

T^w_1/2 est déterminé par l’analyse de la cinétique de relaxation de pression. Cependant, on notera que la détermination de V, A et e est nécessaire pour avoir accès à la conductivité hydraulique membranaire de la cellule. V et A peuvent être déterminés plus ou moins facilement selon les tissus, soit par mesure directe sous microscope (possible sur l’épiderme d’oignon, par exemple) ou à l’issu d’analyses histologiques sur coupes fines de tissu similaire et il s’agira alors d’une estimation.

La sonde à pression sert également à quantifier le rapport dP/dV nécessaire à la mesure de e. Alors que dP est directement enregistré par la sonde, l’opérateur doit mesurer le volume de solution injecté ou aspiré de la cellule (dV) à partir du déplacement du ménisque eau/huile dans le capillaire de la sonde.

La conductivité hydraulique membranaire ainsi mesurée varie de 1 à 1000 10^-8 m s^-1 MPa^-1 selon le type cellulaire et l’état physiologique de la cellule.

Les aquaporines et Lp

Les aquaporines sont responsables de la grande perméabilité à l’eau des membranes. Ces protéines appartiennent à la grande famille des MIPs (Major Intrinsic Proteins, 25-34 kDa[5]). Elles sont constituées de 6 domaines transmembranaires connectés par 5 boucles et formant un pore central.

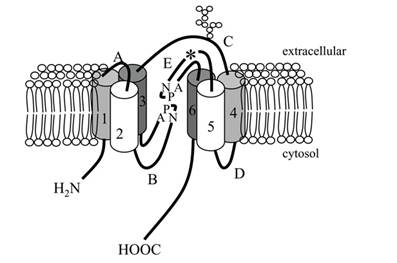
Figure 7. Schéma d’une aquaporine insérée dans une membrane. Six domaines transmembranaires connectés par 5 boucles délimitent un pore central. La présence de motifs NPA au sein du canal empêche les interactions entre molécules et les motifs Ar/R sont responsables de la grande sélectivité du canal. (Zardoya 2005 Bio Cell)

Les MIPs sont des canaux perméables à l’eau ou à des petites molécules non chargées (urée, glycérol, CO₂…). De plus, des séquences très conservées (ex : NPA, Ar/R) affleurant dans le pore central rendent ces canaux spécifiques à une molécule, et l’étroitesse du canal implique que les molécules transportées passent en file indienne, prévenant toute interaction d’autres molécules (pas de passage simultané eau et soluté). Une grande partie des MIPs sont des canaux à eau (d’où le nom « aquaporines ») et il a été montré qu’elles étaient responsables de la grande perméabilité à l’eau des membranes, car si on les bloque, Lp diminue de 75 à 95%. Ainsi la conductivité hydraulique membranaire Lp dépend fortement de la présence mais aussi de l’activation de ces canaux à eau.

Chez toutes les espèces végétales, les MIPs constituent une grande famille multigénique (35 gènes chez Arabidopsis, 55 chez le peuplier, 42 chez le chêne) et sont distribuées en différentes classes dont les principales sont les PIPs (plasma membrane intrinsic proteins) et les TIPs (tonoplast intrinsic proteins) mais il y a aussi (les SIPs, les NIPs et les XIPs). Ainsi toutes les membranes cellulaires, en plus de la membrane plasmique, contiennent des aquaporines. Les PIPs sont principalement localisées sur la membrane plasmique, les TIPs sur le tonoplaste.

La mise en évidence de ces protéines responsables du transport de l’eau à travers les membranes biologiques a induit une re-visitation du fonctionnement hydrique et de tous les flux d’eau dans la plante. En effet, d’un processus physique passif, la perméabilité à l’eau via les aquaporines devient une propriété activement régulée à court terme au niveau moléculaire, via par exemple la quantité de protéines (via la transcription et la traduction), leur activation, leur blocage, etc. On notera cependant que le transfert proprement dit reste un processus passif et que les aquaporines n’interviennent pas dans la nature des forces induisant les transferts hydriques (gradient de potentiel hydrique).

[4] au contraire d’une une solution hypotonique, la solution hypertonique est caractérisée par une concentration en solutés supérieure à celle de la cellule

[5] kDa signifie kilodalton = 1000 dalton, le dalton étant une unité de mesure de masse moléculaire, utilisée pour caractériser la taille des protéines. Une mole de protéine de 1kDa pèse 1000 g.