La capillarité et les plantes
La circulation de la sève xylémienne
Les phénomènes capillaires jouent un rôle capital dans l'ascension de la sève dite « brute ». La circulation de l’eau au sein d’une plante est un phénomène complexe. La théorie actuelle, largement acceptée, qui explique le mieux la montée de sève via le réseau xylémien est celle de la tension-cohésion (cf. Chapitres II.7, II.8 et II.9). Le principe de cette théorie est que l’évaporation de l’eau au niveau des feuilles (passage de l’eau de l’état liquide à l’état gazeux) va tirer la colonne d’eau et la mettre sous tension. Les forces de cohésion entre les molécules d’eau vont permettre de maintenir un continuum liquide entre le sol et les feuilles malgré les niveaux de tensions très importants. Dans cette théorie, la capillarité joue un rôle notamment via la loi de Jurin car c’est la "pompe" qui va tirer l’eau au niveau des feuilles.
Pour l’illustrer, appliquons la loi de Jurin (Eq. 10) aux « capillaires » observables au niveau des plantes. A partir des données de diamètre des vaisseaux conducteurs du xylème (par exemple d’un rayon de 25mm) et en considérant un mouillage maximal (q = 0), la loi de Jurin conduit à une hauteur de montée de la sève de 57,08 cm. Or les arbres, et parfois très grands (plus de 100 m pour certains), existent et fonctionnent parfaitement ! Dans la réalité les vaisseaux hydrauliques ne débouchent pas directement à l’air libre car l’évaporation de l’eau liquide s’effectue via des microfibrilles cellulaires au sein des chambres stomatiques. Ces microfibrilles créent des ménisques dont le rayon est de l’ordre de 10 nm (1 nm = 10-9 m). Appliquons alors la loi de Jurin (Eq. 10) à ces microménisques. La hauteur d’eau admissible est alors de 1427 m et induit une dépression (Eq. 8) entre l’air et l’eau contenue dans la feuille de -14 MPa. Bien sûr, aucun arbre n’atteint cette taille, car d’autres contraintes, mécaniques et fonctionnelles, vont jouer un rôle prépondérant et limiter leurs tailles.
Interactions eau-feuille – Capillarité externe
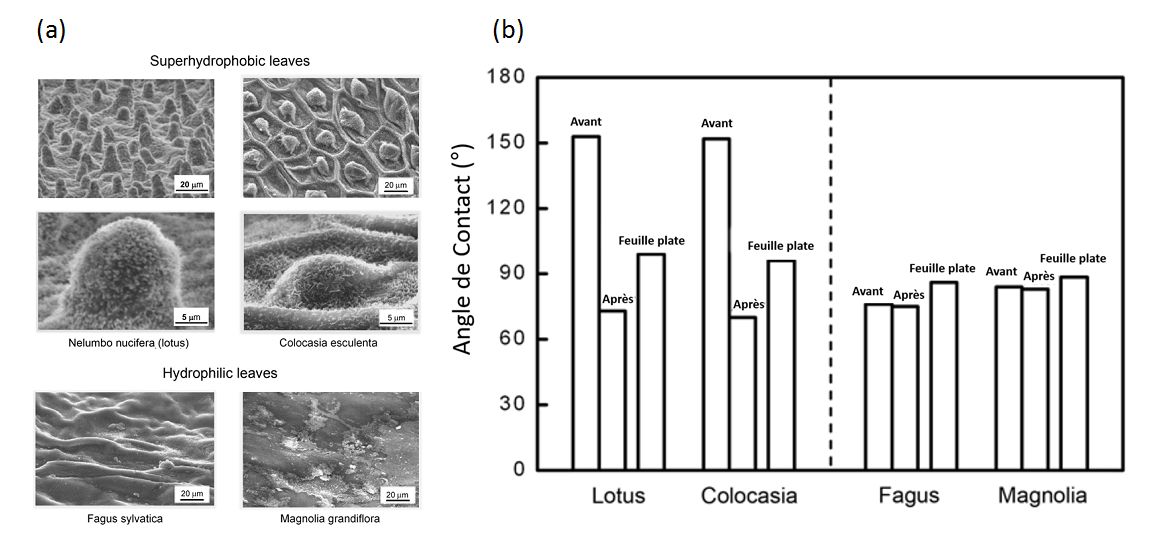
Figure 12 – Images obtenues par microscopie à balayage électronique des rugosités de surfaces de certaines feuilles (a) et conséquences sur l’angle de contact à l’équilibre q (b – « Avant »). Lorsque la couche superficielle des feuilles est enlevée (avec le l‘acétone), les angles de contact diminuent fortement pour les feuilles super hydrophobes (b – « Après »). L’estimation de l’angle de contact sans rugosité (b – « Feuille plate ») conduit au même résultat. Ces figures illustrent le rôle prépondérant de l’état de surface (cire et rugosité) sur la mouillabilité des feuilles très hydrophobes (Lotus et Colocasia) – Images issues de Bhushan and Jung, 2008
Le contact d’un liquide avec des feuilles entraîne un phénomène de mouillage conditionné par la nature du liquide (eau plus ou moins pure, pesticide ou autre intrant agricole fluide) et par les propriétés mouillantes de la surface des feuilles. Celles-ci varient en fonction de plusieurs facteurs, principalement la génétique (espèce, variété), le stade de développement, et l’état de santé du végétal. Ainsi l’on trouve des espèces au comportement mouillable « modèle » comme le lotus sacré (Nelumbo nucifera) dont les feuilles ont des propriétés autonettoyantes, résultantes de la superhydrophobie de leur surface (Bhushan and Jung, 2008): les gouttes à la surface des feuilles de lotus ont un angle de contact q supérieur à 150°, elles roulent donc sur la surface en emportant les poussières et pathogènes présents à la surface. A l’opposé, les feuilles de hêtre commun (Fagus sylvatica) sont hydrophiles : les gouttes d’eau à leur surface forment un angle de contact q systématiquement inférieur à 90°. Différents génotypes d’une même espèce ont par ailleurs des feuilles à la mouillabilité variable. Ainsi on trouve pour de gouttes d’eau à la surface de pommiers de différentes variétés, un gradient de la valeur d’angle de contact de l’ordre de 25° dans des conditions identiques d’apport d’eau. La surface des feuilles évolue également au cours de leur développement : une feuille jeune est généralement dénuée de cire cuticulaire diminuant l’hydrophobie (Bringe et al., 2006) et souvent pourvue de nombreux trichomes (i.e. les « poils » des feuilles). Ces derniers, en nombre suffisant, augmentent la rugosité de la surface des feuilles et par suite l’hydrophobie de la surface. Le développement d’un pathogène comme l’oïdium (Podosphaera aphanis) modifie la mouillabilité de sa feuille hôte : des feuilles de fraisier (Fragaria vesca) acquièrent des propriétés superhydrophobes conduisant à un lessivage des spores par aspersion d’eau (Gadoury et al., 2010).
Les considérations précitées sur la mouillabilité des feuilles ne tiennent pas compte d’une caractéristique importante : l’inclinaison des feuilles qui, dans la réalité, est très rarement horizontale, et l’apport continu d’eau (par condensation, précipitation ou aspersion), introduisant des conditions supplémentaires à l’adhésion d’une goutte sur une feuille. Considérons par exemple un volume d’eau déposé sur un support horizontal. La goute formée se caractérise alors par un rayon (R) et un angle d’équilibre (q) (Figure 7). Lorsque le plan est incliné, comme illustré sur la figure 8a, la goutte va se déformer et à partir d’un angle critique, a, la goutte peut glisser car les forces d’adhésion vont être plus petites que la force de gravité. Ainsi, et pour une goutte donnée de rayon R avant dépôt sur le support, le seuil de stabilité d’une goutte peut être établi en fonction de l’angle d’inclinaison du substrat, a, et de la force d’adhésion de la goutte sur le support, g :
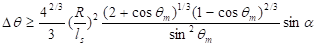 Eq. 12
Eq. 12
Où ls est la longueur capillaire décrite plus haut et qm un angle moyen défini tel que ![]() et
et ![]() . Si l’hystérésis est inférieure au membre de droite de l’équation, la goutte glissera par effet d’inclinaison (Quere et al., 1998). L’application de cette équation permet d’établir pour un rayon (R) et un angle d’inclinaison donnés, les conditions d’adhésion (angle q et hystérésis Dq) à partir desquels la goutte glisse sur son support.
. Si l’hystérésis est inférieure au membre de droite de l’équation, la goutte glissera par effet d’inclinaison (Quere et al., 1998). L’application de cette équation permet d’établir pour un rayon (R) et un angle d’inclinaison donnés, les conditions d’adhésion (angle q et hystérésis Dq) à partir desquels la goutte glisse sur son support.
Par exemple prenons un goutte d’eau de rayon 0,5 mm posée sur un support vertical comme une vitre (a = 90°). En fonction de l’état de surface de la vitre, des conditions très hydrophobes (q > 150°) ou plus ordinaires (q <90°), la goutte va glisser ou se déformer mais rester immobile (Figure 13). Il apparaît également que pour les mêmes caractéristiques de mouillage (angle q et hystérésis Dq), les grosses gouttes glisseront plus facilement que les petites gouttes (Figure 14).
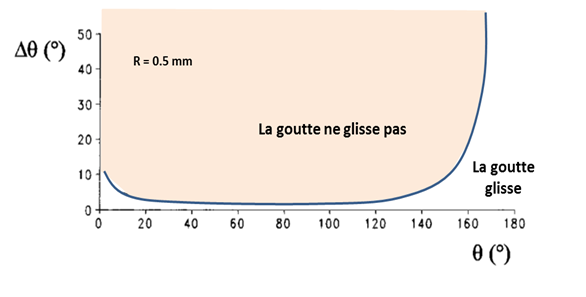
Figure 13 : Illustration des conditions de mouillage (angle q et hystérésisDq) sur le mouvement d’une goutte de 0.5 mm de rayon déposée sur un support vertical (Quere et al., 1998).
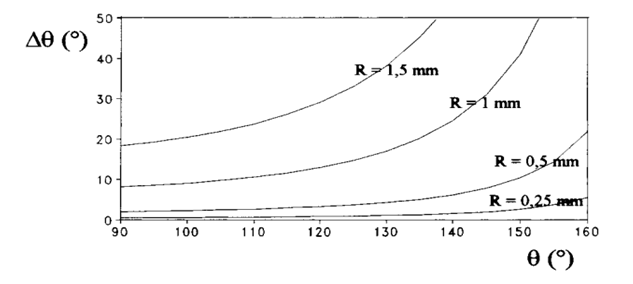
Figure 14: Illustration de l’influence de la taille d’une goutte sur son mouvement sur un support vertical en fonction des conditions de mouillage (angle q et hystérésisDq) (Quere et al., 1998).
L’utilisation de cette équation permet d’établir des tendances pour un support idéal. Dans la réalité, une goutte sur une feuille par exemple, des mécanismes physiques supplémentaires doivent être pris en considération, telles la rigidité et l’élasticité du pétiole, la surface du limbe, et la zone précise de la feuille où la goutte est placée. Le problème devient alors excessivement complexe et nécessite une approche de modélisation poussée.

Références bibliographiques
Aryal, B. and Neuner, G., 2010. Leaf wettability decreases along an extreme altitudinal gradient. Oecologia, 162(1): 1-9.
Bhushan, B. and Jung, Y.C., 2006. Micro- and nanoscale characterization of hydrophobic and hydrophilic leaf surfaces. Nanotechnology (Print), 17(11): 2758-2772.
Bhushan, B. and Jung, Y.C., 2008. Wetting, adhesion and friction of superhydrophobic and hydrophilic leaves and fabricated micro/nanopatterned surfaces. Journal of Physics: Condensed Matter, 20(22): 1-24.
Bringe, K., Schumacher, C.F.A., Schmitz-Eiberger, M., Steiner, U. and Oerke, E.-C., 2006. Ontogenetic variation in chemical and physical characteristics of adaxial apple leaf surfaces. Phytochemistry, 67(2): 161-170.
Broch, P.H., 2016 Cours "Mécanique des Fluides" v.4.0 pp. P. 32.
Cassie, A.B.D. and Baxter, S., 1944. Wettability of porous surfaces. Transactions of the Faraday Society, 40(0): 546-551.
Christensen-Dalsgaard, K.K., Tyree, M.T. and Mussone, P.G., 2011. Surface tension phenomena in the xylem sap of three diffuse porous temperate tree species. Tree Physiology, 31(4): 361-368.
de Gennes, P.-G., 2002. Gouttes, bulles, perles et ondes. Paris : Belin, Paris.
Gadoury, D.M. et al., 2010. Initiation, Development, and Survival of Cleistothecia of Podosphaera aphanis and Their Role in the Epidemiology of Strawberry Powdery Mildew. Phytopathology, 100(3): 246-251.
Gondrand, C., 2006. Analyse des transferts d’eau dans les micropiles à combustible (Analysis of water transfers in micro fuel cells). PhD Thesis, Insititut National Polytechnique de Toulouse.
Leca, A., 2011. Contribution à l'étude de la durée d'humectation au sein d'un couvert de pommier, Université Blaise Pascal (Clermont Ferrand 2), 327 p. pp.
Noblin, X., 2011. Plants, drops, jets and grains: a few problems at liquid or elastic interfaces, Université Nice Sophia Antipolis.
Quere, D., Azzopardi, M.J. and Delattre, L., 1998. Drops at rest on a tilted plane. Langmuir, 14(8): 2213-2216.
Wenzel, R.N., 1936. Resistance of solid surfaces to wetting by water. Industrial & Engineering Chemistry, 28(8): 988-994.
Zisman, W.A., 1964. Relation of the Equilibrium Contact Angle to Liquid and Solid Constitution. In: F. Fowkes (Editor), Contact Angle, Wettability, and Adhesion. Advances in Chemistry. AMERICAN CHEMICAL SOCIETY, Washington, DC, pp. 1-51.
Sommaire :
- I. OUTILS ET CONCEPTS DE BASE
- II. ETATS ET TRANSFERTS HYDRIQUES DANS ET À TRAVERS LA PLANTE
- II.1. La cellule en tant que compartiment hydrique
- Introduction : la cellule végétale vivante
- Le potentiel hydrique de la cellule et ses composantes.
- Relation potentiel hydrique – volume cellulaire : le diagramme de Höfler
- L’osmorégulation
- Les transferts d’eau transmembranaires
- Importance des relations hydriques pour l’expansion cellulaire
- Mesure des composantes du potentiel hydrique cellulaire
- Références bibliographiques
- II.2. Anatomie des voies de transfert de l’eau dans la plante
- II.3. L'eau dans les tissus et les organes de la plante et ses méthodes de caractérisation
- II.4. L’absorption de l'eau du sol par les racines
- II.5. La transpiration foliaire
- II.6. Transferts et états hydriques dans le continuum Sol-Plante-Atmosphère
- II.7. L’architecture hydraulique, la cavitation et l’embolie des plantes
- II.8. Un modèle simple de fonctionnement hydrique à l'échelle de la plante entière. Application pour un arbre
- II.9. Les flux de sève dans la plante : couplage entre xylème et phloème, modélisation
- II.10. L’eau et le métabolisme carboné : C3/C4, CAM ; efficience de l’eau
- II.1. La cellule en tant que compartiment hydrique
- III. FONCTIONNEMENT DES VEGETAUX EN SITUATION DE STRESS LIE A L’EAU
- III.1. Les végétaux face à la sécheresse
- III.2. Efficience agronomique de l’eau
- Les composantes de l’efficience d’utilisation de l’eau par les cultures.
- Nécessité de quantifier séparément Evaporation du sol et Transpiration des plantes
- Les interactions entre nutrition azotée et alimentation hydrique, conséquence sur l’efficience d’utilisation de l’eau par les cultures.
- Références bibliographiques
- IV. AGRONOMIE DE L’EAU
Dans le chapitre :





