Le potentiel hydrique

II. LE POTENTIEL HYDRIQUE

Nous venons d’examiner un processus d’échange hydrique entre deux compartiments, résultant d’une différence de pression osmotique. Dans le DRPe , bien d’autres flux d’eau existent, qui ne s’expliquent pas par des différences de pression osmotique (par exemple le flux de sève « brute » ou xylémienne à travers l’appareil conducteur). Si donc on veut rendre compte des différents types d’échanges d’eau dans le DRPe il faut disposer d’une grandeur plus générale qui englobe toutes les causes de déplacement de l’eau entre deux points du sol-plante-atmosphère (CSPA) et pas seulement le cas de la pression osmotique. Après une longue période durant laquelle de multiples grandeurs, hétérogènes, ont été proposées, la notion de « potentiel hydrique » s’est imposée, autour des années 70, en tant que variable physique rendant compte des mouvements de l’eau dans le CSPA, quelle que soit leur origine. Ce potentiel hydrique dérive d’une grandeur thermodynamique bien connue en physico-chimie : le potentiel chimique. 

Il est donc nécessaire de commencer par présenter succinctement cette notion de potentiel chimique mais aussi les principaux concepts thermodynamiques qui déterminent les conditions de son utilisation : les concepts de système, d’état d’un système et de travail (ou d’énergie). L’approche suivie ici se veut assez intuitive et ignore les nombreuses démonstrations et la formulation mathématique qu’exigerait une approche théorique plus complète. Le lecteur intéressé pourra se reporter à différents ouvrages tels Slatyer 1967, Atkins 2000, Nobel 2002, Kirkham 2004 .

 

II.1 Rappels de quelques notions de thermodynamique : système, compartiment, environnement

Système

En thermodynamique, on appelle système « une portion d’espace limitée par une surface réelle ou fictive, où se trouve la matière étudiée » (Thellier et Ripoll, 1992). L’espace qui n’est pas dans le système s’appelle son « environnement » ou son « milieu extérieur » (figure 15a). La distinction entre système et milieu extérieur est arbitraire et dépend de l’échelle à laquelle on se place et de ce sur quoi porte notre intérêt. Par exemple, on peut considérer une cellule, un organe ou même une plante entière comme formant un seul système ou un seul compartiment. Une fois défini, le système ou le compartiment est donc un volume de matière considéré comme homogène, à l’intérieur duquel on peut définir des grandeurs caractéristiques propres à l’ensemble. Par exemple on dira que la température du système est de 20°C, qu’il contient telle quantité d’eau, ou telle quantité de matière végétale. Chacune de ces grandeurs physiques ou autres a une valeur unique pour l’ensemble (compartiment) considéré. Une fois ce choix fait, l’environnement en résulte : si le système est une cellule, son environnement pourra être constitué d’autres cellules ou d’un milieu physico-chimique particulier (culture de cellules) mais lui aussi sera souvent considéré comme formant un tout caractérisé par un ensemble de grandeurs pouvant être ou non variables dans le temps.

Dans le DRPe, le mot compartiment est emprunté à l’analyse compartimentale, approche très utilisée en physiologie animale et végétale (Chevallier 1984). Ce terme à deux acceptions : soit il est l’équivalent du mot « système » tel que défini ci-dessus, soit il est un « sous-système ». Dans ce dernier cas, il y a plusieurs compartiments dans un même système (fig. 15b). Par exemple on dira que le sol, la plante et l’atmosphère forment les 3 principaux compartiments du CSPA, entre lesquels circulent des flux d’eau. Les mots « système » et « compartiment » sont donc relatifs et dépendent de l’échelle à laquelle on se place.

Frontière

Le système est séparé du milieu extérieur par une frontière : la membrane cytoplasmique pour une cellule, l’épiderme pour une feuille. La nature des frontières est primordiale, puisqu’elle va déterminer la nature des échanges d’énergie et de matière entre compartiments d’un même système ou entre le système et son environnement. S’il peut y avoir des échanges de matière à travers la frontière qui sépare le système et le milieu extérieur, le système est dit « ouvert » ; sinon, il est dit « fermé » mais aussi « isolé ». Un système fermé n’échange que de l’énergie avec l’extérieur, par exemple de la chaleur. Un système isolé n’échange plus rien, ni matière ni énergie avec l’extérieur. Dans le Drpe, le sol, la plante et l’atmosphère peuvent être considérés comme les compartiments du CSPA qui échange, en particulier, de l’énergie, de l’eau et toutes sortes de substances à travers ses frontières.

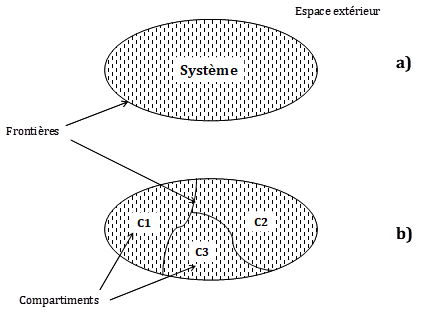
Figure 15. Système, compartiment, frontière en thermodynamique. a) Un système est un volume limité par une surface, fictive ou réelle, qui forme une frontière avec l’extérieur (ou environnement). b) Un système peut être divisé en sous-systèmes ou compartiments (C1, C2, C3) séparés par des frontières internes qui peuvent être de natures différentes entre elles et différentes de la frontière extérieure.

 

Les frontières entre compartiments d’un même système ne sont pas nécessairement de même nature. Ainsi, alors que la frontière entre les racines et le sol correspond à une discontinuité structurale importante, il est clair qu’il n’en va pas de même si l’on cherche à définir une « frontière » entre les racines et l’ensemble « tige-feuilles » d’une même plante. Ces frontières sont en effet définies de façon arbitraire en fonction de l’objectif poursuivi et elles présentent par conséquent des propriétés très différentes, en particulier vis à vis du transport de l’eau.

·        États  thermodynamiques d’un système (ou d’un compartiment)

En thermodynamique, on définit l’état énergétique d’un système par un certain nombre de variables dites « d’état ». Par exemple un compartiment contenant un seul gaz sera entièrement défini si l’on connaît 3 des 4 variables de l’équation d’état d’un gaz parfait (cf. chap. I.1). S’il faut déjà 4 variables pour définir un système aussi simple qu’un gaz enfermé dans un volume, on imagine aisément que caractériser de la même façon un système biologique est quelque chose de très compliqué. On en est donc souvent réduit, dans ce cas, à se limiter à certaines des propriétés du système biologique étudié (propriétés physiques, chimiques, physiologiques, anatomiques, etc.) qui sont supposées les plus importantes pour le caractériser du point de vue choisi. Ainsi quand on fait la mesure du potentiel hydrique d’une feuille (Cf. Chap. II.3) on accepte que celle-ci se réduise à un seul compartiment caractérisé, du point de vue de son état hydrique, par la valeur de ce potentiel hydrique « global ». Si l’on veut comparer deux feuilles d’une même plante ou une feuille et une racine, cette simplification suffit. Par contre si l’on veut étudier plus finement l’état de l’eau (sa « compartimentation », dans une feuille par exemple), plusieurs mesures locales seront alors nécessaires.

Les variables d’état sont de deux sortes : intensives ou extensives. Les variables extensives varient proportionnellement à la quantité de matière présente : c’est le cas de la masse. Leurs quantités sont additives : la masse de deux systèmes est la somme de la masse de chacun d’eux. Au contraire, les variables intensives ne sont pas additives.  C’est le cas de la température, de la pression, de la concentration : mélanger un litre d’eau à 30 °C avec 1 litre d’eau à 10 °C ne produit pas de l’eau à 40 °C mais à 20°C. La concentration en sel de l’eau de mer est la même (si on suppose qu’il y a eu homogénéisation) quelle que soit la taille de l’échantillon qu’on mesure - une cuillérée ou un bassin - ; par contre les quantités de sel seront différentes. Le potentiel chimique et le potentiel hydrique sont des variables intensives.

Un système peut être formé d’une ou de plusieurs phases au sens physique (chap. I.1) : ainsi un mélange d’eau et de glace dans un récipient fermé est, à un moment donné, un système qu’on peut parfaitement définir et dont on pourra prévoir l’évolution dans des conditions données si l’on connaît les quantités présentes dans chacune des phases, la température et la pression dans le système au départ. Un système est à l’équilibre avec son environnement quand son état énergétique reste constant en fonction du temps. 

En fin de nuit, une plante peut être en équilibre hydrique avec le sol (cf. Chap. II.6), le potentiel hydrique étant le même dans toute la plante : il n’y a alors plus de flux d’eau échangé entre les deux.

Si son état énergétique évolue, on dit que le système change d’état. Dans la réalité, un système biologique a de multiples propriétés chimiques, physiques, physiologiques, mécaniques,… Cependant, en général, dans les applications de la thermodynamique utilisées dans le Drpe, on ne peut prendre en compte qu’une très faible partie de cette complexité. On doit ensuite vérifier que la simplification du système est bien acceptable par rapport à la question posée.

·        Energie et travail

En thermodynamique, la définition simplifiée du terme « énergie » est la capacité d’effectuer un travail mécanique, (c’est à dire par un processus équivalent à une force qui se déplace sur une certaine distance (Atkins, 2000)) ou de libérer de la chaleur. Voici différents exemples de production de travail ou de chaleur, donc d’échange d’énergie :

- expansion d’un gaz qui repousse un piston en soulevant un poids ou contre une pression extérieure

- augmentation de la surface d’échange air-eau ; c’est ce qui se passe au niveau des poumons : chaque inspiration entraîne une augmentation de la surface d’échange entre l’air et les alvéoles pulmonaires

- libération de chaleur au cours d’une réaction chimique exothermique, la respiration végétale par exemple ; il peut parfois s’agir de très grandes quantités d’énergie (cas des explosifs)

- déplacement d’une masse liquide entre deux positions de hauteurs différentes. C’est ce que fait la pression osmotique qui entraîne un déplacement de  liquide sur une certaine hauteur.

Dans les systèmes que nous étudions, l’énergie peut être présente et échangée sous différentes formes : chimique, électrique, mécanique, etc.) 

II.2 Expression générale du potentiel chimique d’une substance 

Il est toujours possible en principe, de définir l’état énergétique d’une substance quelconque, quelle que soit la phase gazeuse, liquide ou solide considérée. Les changements d’état physique (température, pression, altitude, …) ou chimique (composition d’une solution) qu’elle pourra subir sont toujours associés à une variation de cet état énergétique. Les flux d’eau entre le sol, la plante et l’atmosphère s’accompagnent tous de différences d’état énergétique de l’eau entre les différents milieux (ou même entre les subdivisions que l’on peut définir dans chacun de ces milieux : couches de sol, racines et feuilles, feuilles et atmosphère par exemple).

La thermodynamique a défini un certain nombre de grandeurs, appelées aussi « fonctions » ou « variables thermodynamiques » qui permettent de définir l’état énergétique d’un corps dans une situation donnée. Le potentiel chimique (souvent noté m), est l’une de ces fonctions ; il est la variable thermodynamique la plus appropriée pour caractériser les variations énergétiques qui se produisent dans toutes sortes de systèmes où se déroulent des processus aussi différents que des réactions chimiques, des variations de composition, l’expansion d’un gaz, les changements d’état d’une substance, etc.) à température et pression constantes.

Le potentiel chimique a la dimension d’une énergie, rapportée conventionnellement à la mole de la substance j considérée (énergie molaire). La grande utilité du potentiel chimique m_j , tient à deux de ses propriétés les plus importantes :

-         d’une part il est définissable quelle que soit la phase considérée (solide, liquide ou gazeuse),

-         d’autre part il constitue le critère d’équilibre entre deux compartiments qui peuvent échanger cette substance (par exemple l’échange d’eau entre le sol et une plante). À l’équilibre, le potentiel chimique de cette substance sera le même dans les deux compartiments, quelles que soient les phases en présence. Ainsi au chapitre I, quand on parle d’équilibre entre eau liquide et eau vapeur, cela signifie que le long d’une ligne de changement de phase (Cf. fig. 5) le potentiel chimique des deux phases est le même pour une température donnée.

 

-         Propriétés de  m_j

- si deux compartiments qui communiquent sont en équilibre, leur potentiel chimique est le même et il n’y a pas de flux de matière entre eux. Si au contraire leur potentiel chimique est différent, ils peuvent (si leur frontière le permet) échanger de la matière jusqu’à égalité des potentiels chimiques.

- si plusieurs phases d’un même compartiment sont en équilibre, le potentiel chimique est le même dans chaque phase et en tout point de chaque phase.

La définition générale du potentiel chimique d’une substance j, est donnée ci-dessous. Pour l’établir il faut passer par une démonstration qui n’a pas sa place ici mais que l’on trouve dans un certain nombre d’ouvrages (voir en particulier Atkins, 2000 et Musy et Soutter, 1991). L’important pour nous est qu’elle explicite, les effets des différents facteurs susceptibles de faire varier l’énergie molaire m_j, de la substance j sous forme d’une somme :

                                       équat. 12 

Chaque terme de l’équation traduit l’effet d’un facteur particulier. Reprenons les un par un pour en préciser la signification :

-                : potentiel chimique de la substance j dans un état de « référence » ou « état standard ». Ce terme fait comprendre un point capital : on mesure toujours des différences de potentiel et non pas des valeurs absolues. Le potentiel chimique, tout comme le potentiel électrique, l’altitude, etc., est une grandeur relative en ce sens qu’elle s’exprime non pas « dans l’absolu », mais par rapport à un état de référence (altitude, pression, température, etc.) donné. Par convention = 0 ; on ne l’écrira donc pas généralement.

-          : correspond, à l’effet de l’activité, a_j, de la substance j (disons pour simplifier que l’activité est une notion proche de la fraction molaire qui intègre les écarts de comportement de la substance réelle par rapport au cas idéal du gaz parfait). Avec R= constante des gaz parfaits ; T= température en Kelvin ;  ln(a_j )= logarithme népérien de l’activité a_j de la substance j.

-               : correspond à l’effet de la pression. V_j = volume molaire de j.

-          : traduit les effets de charges électriques dans le cas où j est un constituant chargé, un ion par exemple. Avec z_j = valence de l’ion (< 0 pour les anions, > 0 pour les cations) ; F, pour « Faraday », constante physique correspondant à la charge électrique portée par une mole d’ion monovalent. DE est la différence de potentiel électrique entre le compartiment où se trouve j, et l’état de référence.

-            : traduit l’effet de l’altitude, avec : m_j = la masse molaire de la substance j, g la constante gravimétrique, h la hauteur par rapport au niveau de référence.

Remarque : le potentiel chimique d’une substance j dérive d’un potentiel thermodynamique appelé énergie libre de Gibbs ou enthalpie libre dont on démontre qu’il est approprié pour décrire l’évolution de systèmes à température et pression constantes (ce qui est approximativement le cas du DRPe). Par définition le potentiel chimique s’exprime par :

                                                                               équat. 13

C’est donc la dérivée partielle de G par rapport à la quantité n_j de substance j lorsque la température, la pression et la proportion des autres substances présentes dans le système considéré restent constantes.

 

II.3 Potentiel chimique de l’eau m_eau , et potentiel hydrique Y

Dans le contexte du DRPe nous ne parlerons que de l’eau. Son potentiel chimique  m_eau  prend alors le nom de potentiel hydrique et est noté Y. Les propriétés générales du potentiel chimique s’appliquent évidemment à l’eau mais pour diverses raisons qui apparaitront plus loin, l’usage s’est imposé d’exprimer Y en unités de pression. Autrement dit l’énergie par mole H₂O impliquée dans la définition du potentiel chimique de l’eau m_eau est rapportée au volume molaire de l’eau. Mais attention : il s’agit toujours du volume molaire de l’eau liquide (environ 18 10^-6 m³).

Différentes méthodes sont actuellement disponibles pour mesurer Y  dans le sol, la plante ou l’atmosphère (voir Chap. II.3), de sorte que Y  est devenu la variable la plus pertinente et la plus pratique pour décrire l’état de l’eau dans le domaine des  relations « plantes-eau ».

Appliquons maintenant l’équation générale (12) ci-dessus au cas de l’eau sachant que le terme « électrique » disparaît puisque l’eau est électriquement neutre (z_eau = 0). L’expression 12 devient donc pour l’eau :

                                          équat. 14

Comme précédemment chacun de ces termes a pour dimension un travail par mole et s’exprime donc en joules par mole (J mole^-1) dans le S.I.

     : correspond au potentiel chimique de l’eau dans l’état de référence. Conventionnellement il s’agit de l’eau pure à la pression atmosphérique à la température T et à l’altitude de référence. On l’a dit plus haut, par convention = 0

RT.ln (a_eau ) = : correspond à l’effet des solutés donc à la pression osmotique p (équat. 8). Le terme a_eau est l’activité de l’eau, grandeur sans dimension qui est égale à la fraction molaire de l’eau dans le cas d’une solution idéale : a_eau = N_eau = n_eau / (n_eau + n_soluté). On remarquera que cette composante du Y est négative ou nulle puisque, ce qui traduit le fait que la présence de solutés diminue le potentiel chimique de l’eau.

V_eau P   : traduit l’effet de la pression sur le potentiel chimique. V_eau est le volume molaire de l’eau soit 18 10^-6 m³ dans le S.I. et P la pression relative c’est à dire comptée en plus ou en moins par rapport à la pression atmosphérique. Ce terme est très important pour décrire l’état hydrique de la plante ou du sol comme on va le voir ci-après.

m_eau gz   : correspond à la composante gravitationnelle du potentiel hydrique. L’altitude z est mesurée par rapport au niveau de référence; m_eau est la masse molaire de l’eau et g la constante gravimétrique.

Remarque. D’une façon moins abstraite, on peut dire que le potentiel chimique de l’eau représente la quantité d’énergie qu’il faudrait apporter à une mole d’eau pour la faire passer de l’état considéré (altitude, pression, liaisons électriques, etc.) à l’état libre de référence (eau libre à la pression atmosphérique et à l’altitude zéro) au cours d’une transformation réversible et isotherme.

Remarque. Relation entre pression osmotique et potentiel chimique de l’eau

Comme on l’a vu, la pression osmotique correspond au second terme de l’expression 14 ci-dessus. La diminution de potentiel chimique de l’eau en présence de solutés est donnée par l'expression :

                                                                   équat. 15

On voit que le potentiel chimique de l’eau dans la solution (mesuré par rapport à l’eau pure) est proportionnel au logarithme de la fraction molaire de l’eau en solution.

Il existe une relation très simple entre le potentiel hydrique m, d’une solution et la pression osmotique p. Si nous rapportons m au volume molaire de l’eau liquide V_eau, , l’équation 15 devient :

                                                     équat. 16

Cette expression qui a la dimension d’une pression correspond à la définition thermodynamique de la pression osmotique. En considérant, comme van ’t Hoff l’avait fait, qu’un soluté dans une solution est analogue aux molécules d’un gaz dans un mélange gazeux, la fraction molaire du solvant est analogue à une pression partielle. La pression osmotique est alors, comme on le voit, égale (au signe près) au potentiel chimique rapporté au volume molaire de l’eau liquide.

Réciproquement, l’expression 16 indique aussi que la pression osmotique est une mesure directe du potentiel chimique m_eau de l’eau d’une solution. Dans le cas d’une solution idéale (diluée) on peut exprimer la pression osmotique p en fonction de la fraction molaire de l’eau :

                                                                             équat. 17 

Remarque. Montrons comment passer de l’expression théorique de p ci-dessus, dans laquelle intervient le logarithme de la fraction molaire de l’eau, N_eau , à celle donnée par la loi de van ‘t Hoff où la pression osmotique est proportionnelle à la concentration en soluté c (cf. équat. 8). Il s’agit de la simple approximation de ln(x) au voisinage de x=1 appliquée à . En effet si on considère une solution diluée, alors n_eau est très grand devant n_soluté de sorte que est très proche de 1 et que le terme ln (N_eau) peut être remplacé par sa valeur approchée  (le premier terme du développement en série de la fonction logarithme népérien). D’ou finalement compte tenu de l’équation 17 :

                                                                                            équat. 18

Où c représente la concentration molaire du soluté. On retrouve bien l’expression de van ’t Hoff (équat. 8).

 

II. 4 Le potentiel hydrique, mesure de l’état énergétique de l’eau dans le végétal, le sol ou l’air

Reprenons la définition du potentiel hydrique comme potentiel chimique de l’eau m_eau, rapporté au volume molaire de l’eau liquide : 

                                 équat. 19

Y a la dimension d’une pression et on a l’habitude de faire apparaître et écrire ses diverses composantes  sous la forme suivante :

                                                                                                                équat. 20

 : potentiel de référence (ou standard), toujours nul par convention. C’est celui de l’eau pure à la température du compartiment considéré (tissu végétal ou tranche de sol), à la pression atmosphérique et à l’altitude de référence z = 0.

Yp = -p: composante osmotique du compartiment étudié (tissu végétal ou tranche de sol). Cette composante est négative si la pression osmotique n’est pas nulle (présence de solutés, sols salés par exemple).

Y_p= P : composante hydrostatique, égale à la pression relative de l’eau (mesurée par rapport à la pression atmosphérique). Qu’il s’agisse d’un tissu végétal ou du sol, cette pression peut être positive ou négative.

- cas de la plante : cette pression est positive dans un tissu végétal turgescent (pression de turgescence des cellules, mais négative le plus souvent dans le xylème, tissu conducteur soumis à des tensions extrêmement basses lorsque la plante transpire.

- cas du sol présentant une nappe d’eau par exemple : la pression est positive en dessous du niveau de la nappe mais négative au dessus, dans la zone capillaire. Lorsque le sol se dessèche, les phénomènes de capillarité et les forces d’adhésion des molécules d’eau sur les particules de sol, la « matrice » du sol, dominent. On parle alors de composante matricielle du potentiel hydrique ; toujours négative elle est souvent notée Y_m.

Y_g=rgz : composante gravitationnelle (ou gravimétrique) qui rend compte de l’effet de l’altitude sur le potentiel total. L’altitude z du compartiment végétal ou du sol considéré est mesurée par rapport au niveau de référence choisi et peut être positive ou négative. Sauf cas particulier (sols saturés sur une grande hauteur ou grands arbres) on ne tient généralement pas compte de cette composante car elle est négligeable par rapport aux deux précédentes. En effet, pour une différence d’altitude de 1 m par exemple entre deux organes d’une plante, la composante Y_g varie de 9810 Pa soit environ 0,01 MPa. Cette variation est négligeable vis à vis des deux composantes majeures Yp et Yp qui interviennent dans la plante et qui sont en général de l’ordre de 0,1 à 1 MPa soit 10 à 100 fois plus grandes.

Remarque. Le principal avantage de la notion de « potentiel hydrique » par rapport au « potentiel chimique » de l’eau, est qu’il s’exprime en unités de pression et non plus de travail. Cela se traduit notamment par le fait que les mesures de potentiel hydrique se ramènent souvent à de simples mesures de pression (cf. la chambre à pression décrite dans le chap. II.3). Ce choix du potentiel hydrique de préférence au potentiel chimique a été fait dans les années 60, notamment pour faciliter l’utilisation de cette nouvelle notion par les biologistes qui utilisaient depuis longtemps les unités de pression (pression osmotique et pression de turgescence) pour caractériser l’état de l’eau chez les végétaux.

Remarque. Aujourd’hui, le terme de potentiel hydrique prévaut presque toujours, mais on peut toujours rencontrer d’autres appellations : tension, déficit de pression (de succion ou de diffusion), tension de succion, force de succion, hauteur capillaire, etc. Il s’agit le plus souvent de synonymes, au signe près et à la nature de la quantité unitaire d’eau considérée. Ainsi lorsque l’on rapporte l’énergie au volume d’eau, le potentiel hydrique s’exprime en pression (c’est la convention retenue) ; si elle est rapportée au poids d’eau, il s’exprime en longueur (m le plus souvent) ; enfin si elle est rapportée à la masse d’eau, l’unité est le J kg ^-1. On trouvera des renseignements détaillés sur ce point dans Slavík (1976).

Néanmoins, le potentiel hydrique Y se trouve généralement exprimé à l’aide de différentes unités de pression, et l’habitude s’est prise dans le DRPe d’utiliser le plus souvent le mégaPascal (MPa) ; plus rarement aujourd’hui, le bar (1bar valant presque une atmosphère). Les équivalences sont les suivantes :

1 bar = 0,987 atm =  0,1 MPa = 10⁵ Pa

·        Expression réduite du potentiel hydrique dans la plante

Pour un échantillon végétal, en négligeant le terme gravitationnel, le potentiel hydrique Ydans la plante s’écrit : 

                                                                             équat. 21

où se rapporte soit à la pression de turgescence des cellules (il est alors positif), soit à la tension de l’eau (pression relative négative) dans l’appareil conducteur (il est alors négatif) et  désigne le potentiel osmotique toujours négatif. On trouve souvent l’écriture équivalente suivante :

                                                                                   équat. 22

·        Expression réduite du potentiel hydrique du sol

Dans le sol, l’absence de membrane semi-perméable fait que le terme  de pression osmotique disparaît le plus souvent. Il faudrait néanmoins en tenir compte dans le cas de sols salés pour exprimer par exemple la pression de vapeur d’eau en équilibre. L’expression générale (équat. 20) se  trouve ainsi simplifiée :

         

      : composante hydrostatique. Positive dans la nappe, elle est négative au dessus où on la désigne souvent comme composante « matricielle » ou « capillaire »

      : composante gravitationnelle. Elle ne joue un rôle significatif que dans les sols proches de la saturation pour traiter par exemple le phénomène de drainage. Ainsi le potentiel hydrique dans le DRPe  où le sol est généralement non saturé se réduit le plus souvent à sa composante matricielle :

                                                                  équat. 23

Le chapitre I.4  revient en détail sur le sol en tant que réservoir d’eau pour les plantes.

·        Le potentiel hydrique de la vapeur d’eau dans l’atmosphère.

Comme indiqué précédemment, les concepts de potentiel chimique et hydrique s’appliquent aux gaz, donc à la vapeur d’eau de l’air dont l’état est entièrement déterminé par la pression partielle p et la température T. Calculer le potentiel hydrique d’une mole de vapeur d’eau à la pression p, revient à calculer l’énergie nécessaire pour l’amener à l’état de référence c’est à dire en équilibre avec l’eau pure à la même température, autrement dit la vapeur à la pression saturante.

Si l’on suppose que la vapeur d’eau est un gaz parfait obéissant à la loi de Mariotte, le volume molaire V à la pression p et la température T s’écrit  :

     

La transformation réversible qui permet de passer de l’état initial (p,V) à l’état final (,) est une compression isotherme. Au cours de cette compression, un accroissement élémentaire de pression dp entraine une diminution de volume dV et nécessite un apport d’énergie dW égal à -p dV. S’agissant d’un gaz parfait, on peut écrire :  d’où l’expression de l’énergie élémentaire mise en jeu :

L’énergie nécessaire pour passer de p à  est obtenue par intégration :

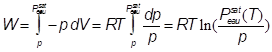               (J mol^-1)           équat. 24

C’est cette quantité d’énergie, perdue par la vapeur d’eau lorsqu’elle est à la pression p par rapport à la pression saturante, qui intervient dans le calcul du potentiel hydrique de la vapeur d’eau.

Rappelons la définition de l’humidité relative de l’air avec les mêmes notations :

                      (%)

L’équation 24 montre que mesurer le potentiel hydrique dans l’air revient à mesurer l’humidité relative HR. Conventionnellement, pour exprimer le potentiel hydrique Y dans la phase gazeuse, on rapporte la quantité d’énergie W ainsi calculée au volume molaire de l’eau liquide V_eau , soit 1,805 10^‑5 m³ mol^-1 à 20°C. L’expression générale du potentiel hydrique dans l’air devient alors :

(Pa)                      équat. 25

 

Remarque : on a vu que dans un système en équilibre, le potentiel hydrique est identique dans toutes les phases qui le composent, la phase gazeuse notamment. Il en résulte que la mesure du potentiel hydrique d’un échantillon de sol ou de plante va pouvoir se faire dans l’air en équilibre avec ces échantillons. C’est le principe des méthodes psychrométriques assez largement utilisées (voir chapitre II.3). Quelle que soit la phase considérée, Y s’exprimera donc toujours en Pascal et les valeurs trouvées sont comparables entre elles.

Remarque : la pression calculée par l’équation 25 correspond à la pression que l’on mesurerait éventuellement dans la phase liquide d’eau pure d’un système en équilibre. Il s’agit le plus souvent dans le DRPe d’une pression virtuelle car les valeurs extrêmement basses (négatives) de potentiel hydrique rencontrées correspondent à des conditions incompatibles avec l’existence d’eau en phase liquide libre.

La figure 16 montre graphiquement la relation entre humidité relative et potentiel hydrique (équation 25) pour deux températures (20°C et 35°C). On remarquera en particulier que la différence de température joue peu. On reviendra souvent à cette relation cruciale.

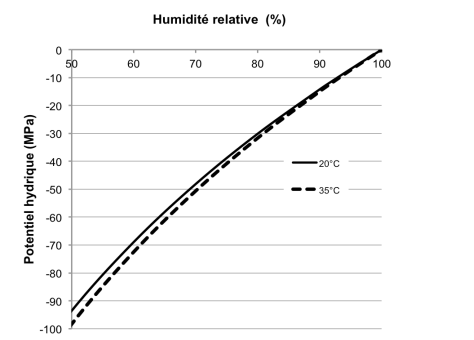
Figure 16. Variation du potentiel hydrique en fonction de l’humidité relative de l’air en équilibre. Effet de la température.

 

Application 1: quel est le Y de la vapeur d’eau dans l’air dont l’humidité relative HR est de 50% et la température T_a = 25°C ?        

Réponse :           Y  =- (8,314 x 298)/18,05 10^-6) ln(50/100) = -95,15 MPa

Application 2 : quel est le potentiel hydrique de la vapeur d’eau de l’air dont l’humidité est de 99% et la température de 25°C ?

Réponse :           Y  =- (8,314 x 298)/18,05 10^-6) ln(99/100) = -1.38 MPa

Comme indiqué plus haut, la température joue peu : ainsi par exemple une humidité relative de l’air de 50% correspond pour un air à 25°C à une valeur d’environ -95,1 MPa du Y, et à -93,6 MPa si la température n’est plus que de 20°C.

Ces exemples montrent deux points importants que l’on retrouvera souvent dans l’étude du DRPe :

- d’une part, une humidité de l’air classique en été, soit 50%, correspond à un potentiel hydrique très bas (presque -100 MPa) alors que dans les feuilles le potentiel hydrique est beaucoup plus élevé (Y  compris entre – 0,1 et – 3 MPa environ). Il y a donc une chute de potentiel extrêmement importante entre la feuille et l’air.

- d’autre part, on voit que le potentiel hydrique d’un air quasiment saturé (99%) correspond néanmoins à une valeur assez basse pour un végétal, valeur voisine de celle appelée « point de flétrissement permanent » (cf. chap. II.5).

·        Convention de signe du potentiel hydrique

Pour comprendre pourquoi la plupart du temps le potentiel hydrique des végétaux, du sol ou de la vapeur d’eau de l’atmosphère est négatif, il faut revenir à la signification énergétique de Y.

On a vu que le potentiel hydrique représente l’énergie qu’il faut fournir à la mole d’eau pour l’amener de l’état où elle se trouve (liée dans une plante ou dans une couche de sol) ou vapeur d’eau dans l’air, à un état standard, celui de l’eau libre à la pression atmosphérique (Y_eau = 0).

- le plus souvent, pour passer de l’état lié à l’état de référence, il faut fournir de l’énergie (comme par exemple pour faire passer un certain volume d’eau du niveau z à un niveau z_f plus élevé), Le potentiel initial est donc négatif. Ainsi par exemple, l’ensemble des organes d’une plante en condition de transpiration est à des potentiels négatifs. De même pour l’eau d’un sol qui n’est pas à saturation. C’est donc le cas le plus fréquent que l’on rencontrera dans le Drpe.

- Il peut arriver exceptionnellement que le niveau d’énergie initial du volume d’eau  soit supérieur à celui de l’état de référence. Le potentiel est alors positif. C’est par exemple le cas de la sève xylémienne soumise à la poussée racinaire ou de la guttation, phénomène de sortie de la sève sous la forme de gouttes sur le pourtour d’une  feuille.

·        Exemples de valeurs du potentiel hydrique dans les différentes parties du CSPA

Le tableau 1 donne quelques exemples d’ordre de grandeur de valeurs courantes de Y et de ses composantes dans les différentes parties du continuum sol-plante-atmosphère (CSPA). Il s’agit là de valeurs habituelles qui montrent :

- d’une part que les valeurs du Y des différentes parties du CSPA sont la plupart du temps négatives. Il y a cependant des exceptions importantes comme on le verra, en particulier pour certains arbres, en période hivernale dans les pays tempérés.

- d’autre part que le Y de la vapeur d’eau de l’atmosphère a des valeurs extrêmement basses par rapport à celles des différentes parties des végétaux et du sol. Autrement dit, les variations de potentiel hydrique correspondant au transport de l’eau dans la phase liquide, c'est-à-dire le long du trajet sol-feuilles, sont très faibles par rapport aux variations de potentiel qui existent dans la partie gazeuse (espaces intercellulaires de la feuille-atmosphère), sur une faible distance de trajet. Cette situation a des conséquences très importantes sur l’alimentation hydrique des plantes.

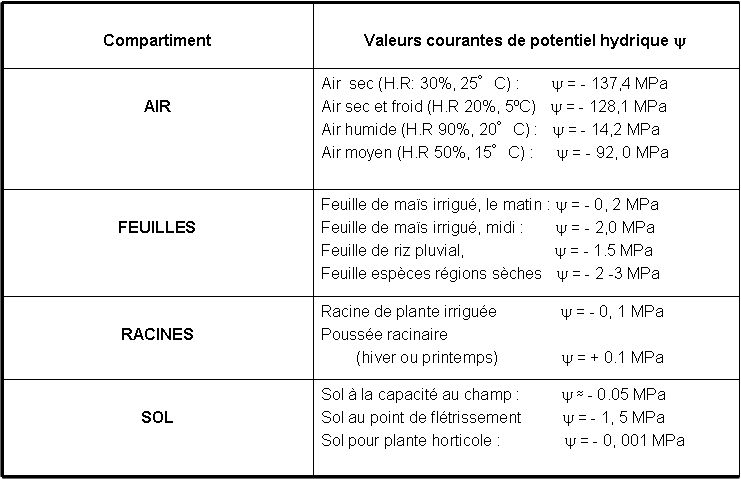
Tableau 1. Exemples de valeurs courantes du potentiel hydrique dans le sol, les plantes ou l’air. Attention ces valeurs sont des ordres de grandeurs en conditions naturelles, pour fixer les idées ; les comparer sans connaître des informations supplémentaires n’apporte rien. Par contre, on voit que globalement les potentiels sont de plus en plus négatifs (sauf cas particuliers comme celui des racines qui en hiver ou au printemps montrent une poussée racinaire qui correspond à des potentiels hydriques positifs) au fur et à mesure qu’on passe du sol vers l’atmosphère. Par ailleurs, un autre fait important est à noter : les potentiels en phase vapeur (dans l’atmosphère) sont beaucoup plus bas que ceux en phase liquide. On verra que cette situation est d’une grande importante dans l’alimentation en eau des plantes.

 

II.5 Le potentiel hydrique, variable déterminant le sens des flux d’eau dans le continuum sol-plante-atmosphère (CSPA) 

Ce paragraphe introduit l’utilisation du potentiel hydrique en tant que variable impliquée dans l’étude des flux d’eau dans le CSPA. Les différences de potentiel renseignent sur le sens des échanges hydriques entre compartiments et permettent dans certains cas de déterminer l’intensité des flux d’eau échangés entre compartiments.

·        Relation entre potentiel hydrique et flux d’eau : loi de Darcy généralisée

Si deux compartiments qui communiquent sont en équilibre hydrique (même Y) alors il n’y a pas de flux d’eau entre eux. Par contre si ces deux compartiments communiquent (à travers une membrane, une paroi ou une surface poreuse, par des capillaires comme ceux formés par les éléments conducteurs,…) et que leur potentiel hydrique n’a pas la même valeur, alors un flux d’eau s’établit entre eux. La notion de Y fournit donc un critère de l’existence d’un flux d’eau entre deux compartiments : celui-ci se fera du compartiment ayant le Y le plus haut vers celui dont le Y est le plus bas.

L’expérience montre que dans les différents milieux considérés dans le CSPA, l’intensité du flux d’eau qui circule entre deux points est souvent proportionnelle à la différence de potentiel hydrique entre ces deux points (voir chap. II.6 et II.8). Cette remarque établit l’analogie formelle entre les transferts d’eau dans le CSPA et les lois physiques de circulation de l’électricité dans les conducteurs par exemple. Ainsi, de même que la loi d’Ohm DV=r*I permet de définir la résistance électrique comme le rapport entre la différence de potentiel électrique DV aux bornes de la résistance et l’intensité I du courant qui circule, on peut écrire une relation analogue pour les flux d’eau :

                                                                                                          équat. 26

où F : flux d’eau circulant entre deux points A et B (m³ s^-1)

Y_A et Y_B : potentiel hydrique aux points A et B respectivement (dans une plante par exemple)

Cette relation définit la résistance hydraulique du tronçon AB : r_AB (MPa m^-3 s). On peut également définir une conductance, qui en est l’inverse Lp_AB = 1/r_AB. Ce formalisme est utilisé principalement entre deux niveaux d’une plante. Dans le sol on l’emploie également sous le nom de loi de Darcy généralisée.

Application : on trouve que chez une plante : Y_racines = - 0,2 MPa et Y_feuilles= - 1,2 MPa ; la valeur du courant de sève circulant entre les racines et les feuilles est de 2 10^-7m³  s^-1. Donner la valeur de la résistance globale racines-feuilles. En appliquant la relation 31 on a tout de suite 

                                                               r = [(- 0,2 - (- 1,2)]/ 2. 10^-7= 0,5 10⁷ MPa m^-3 s

Notons que résistance et conductance peuvent varier aussi bien dans la plante que dans le sol avec le potentiel hydrique. De même, la cavitation et l’embolie des éléments conducteurs augmentent leur résistance. En ce qui concerne le sol, l’assèchement qui accompagne la diminution du potentiel hydrique correspond au drainage des pores de plus en plus fins. Il en résulte une augmentation drastique de la résistance hydraulique.

Pour les flux gazeux, dont l’approche physique était établie depuis plus longtemps, mais sur d’autres bases, on a gardé l’habitude de les exprimer en fonction de différences de concentration en vapeur d’eau et non pas de potentiel hydrique. En conséquence les unités avec lesquelles on exprime les résistances en phase gazeuse et celles en phase liquide ne sont pas les mêmes.

·        Mise en garde à propos de l’utilisation de l’équation :                        flux  = DY/R

Les équations présentées dans ce chapitre constituent la base de modèles décrivant les transferts d’eau dans le CSPA (Cf. Chap. II.6). Il convient à ce stade d’alerter le lecteur sur une des caractéristiques des milieux étudiés ici : qu’il s’agisse de la plante, du sol ou de l’atmosphère, on a affaire à des milieux essentiellement hétérogènes et dont les propriétés varient dans le temps.

Dans de tels milieux (sol, plante, etc.), différentes voies de passage peuvent s’offrir en parallèle au transfert de l’eau, ce qui peut entraîner l’apparition de phénomènes particuliers comme par exemple l’existence d’itinéraires privilégiés entourant des ilots plus ou moins isolés. Le formalisme ohmique, même s’il continue à s’appliquer à petite échelle dans chacun des domaines localement homogènes, ne suffit plus pour décrire précisément la dynamique des transferts à une échelle plus globale. C’est le cas par exemple dans des sols comportant des agrégats individualisés (figure 17). La limite de l’approche simple apparaît encore plus clairement si l’on pense à la plante dans laquelle deux flux de sève de sens opposé coexistent : sève brute montante, sève élaborée descendante. Il est clair que cette situation ne saurait être décrite à l’aide d’une seule valeur de potentiel hydrique. D’une façon générale il est important dans ce genre de situation essentiellement hétérogène de faire l’analyse des voies de passage de l’eau et des mécanismes mis en jeu. On verra un exemple de mise en œuvre de cette approche type « milieu complexe » dans la description des flux de sève dans la plante (Chap. II.9).

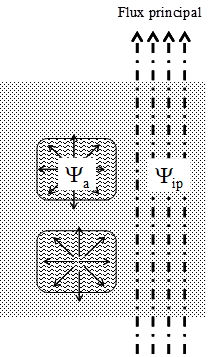
Figure 17. Représentation schématique des trajets possiblement empruntés par l’eau dans un sol de structure hétérogène. Dans cet exemple on imagine que le flux d’eau est globalement vertical vers le haut et transite majoritairement dans des itinéraires privilégiés. Certains agrégats situés plus ou moins à l’écart de ces itinéraires peuvent cependant contribuer au flux global. On doit alors admettre que le potentiel hydrique au centre des agrégats Y_a n’est pas identique à ce qu’il est dans les voies principales voisines Y_ip. Ce type de distribution non uniforme du potentiel hydrique doit se retrouver très généralement lorsqu’on considère des milieux hétérogènes, parmi lesquels les plantes notamment.

Enfin, les méthodes de mesure du potentiel hydrique ou des flux d’eau sur le terrain, bien que de plus en plus précises, restent entachées d’erreurs plus ou moins grandes. Ces limites méthodologiques entrainent des marges d’erreur relativement importantes notamment dans la détermination des variables d’état comme le potentiel hydrique ou des propriétés hydrauliques des différents milieux (résistances, perméabilités, …).