Première expression de la transpiration

Soit E la transpiration par unité de surface de la feuille, en g m^-2s^-1. Elle est proportionnelle à la différence (χ_i – χ_a) d’humidité absolue entre l’air interne à la feuille et l’air externe, et inversement proportionnelle à la somme (r_a + r_s) des résistances qui s’opposent à la diffusion de vapeur d’eau[7] (figure 5). Si les deux faces de la feuille ont les mêmes densités stomatiques, on peut écrire :

                    E =2. (χ_i – χ_a)/ (r_a + r_s)                                              (2)

où r_a et r_s sont en s m^-1

L’air interne est très proche de la saturation à température foliaire[8], on a donc d’après (1) χ_i= e_s(T_f). (M_e/RT_f) et χ_a = e_a.(M_e/RT_a), ce qui permet d’écrire (2) sous la forme :

                    E = 2.(M_e/RT_a). (e_s(T_f) - e_a)/ (r_s + r_a)                         (3)

en supposant RT_f = RT_a (une erreur relative inférieure à 1 % pour T_f -T_a < 3 K)

L’expression (3) est relativement facile à calculer lorsqu’on connaît les températures de la feuille T_f  et de l’air T_a,  l'humidité de l’air e_a, et les résistances de la feuille r_s et r_a .

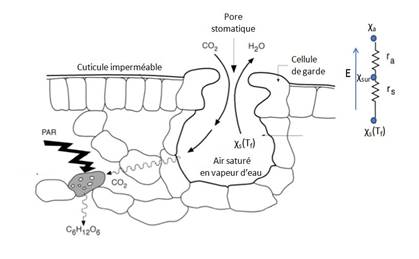
Figure 5. Diffusion de la vapeur d'eau à travers l'épiderme

Mais comme T_f n’est pas facile à mesurer, on a cherché à la calculer en utilisant le bilan énergétique de la feuille, pour pouvoir calculer E en fonction des seules variables externes. La transpiration est limitée par l’énergie disponible pour évaporer l’eau des cellules, connue sous le nom de chaleur latente de vaporisation λ, élevée chez l’eau (λ~2,45 MJ kg^-1) . Cette forte valeur de λ représente environ 600 cal/g : il faut 6 fois plus d'énergie pour évaporer un gramme d'eau que pour le chauffer de 0 °C à 100 °C. Ainsi, le rayonnement net absorbé par une feuille est dissipé sous forme de chaleur latente et de chaleur sensible. En explicitant ce bilan énergétique, on peut éliminer la température foliaire pour exprimer la transpiration en fonction des seules variables climatiques.