Compléments

C1 Expression des flux de gaz (CO₂ et H₂O) échangés par la feuille

C’est par le mécanisme de diffusion gazeuse que les molécules CO₂ ou H₂O circulent entre l’intérieur de la feuille et l’atmosphère. Ce phénomène a été bien décrit par les physiciens et il obéit à un formalisme de type ohmique, c’est à dire calqué sur les lois de l’électricité. La forme générale des lois de la diffusion gazeuse est la suivante :

                (mol_J m^-2 s^-1)                                                                       (équat. 29)

équation qui exprime que le flux  de l’espèce gazeuse J qui transite entre les niveaux A et B par unité de surface (densité de flux) est proportionnel à la différence de concentration de J (fraction molaire) entre A et B d’une part, inversement proportionnel à la résistance à la diffusion sur ce trajet d’autre part r_AB [3](figure 20). La résistance du trajet AB est fonction de la géométrie du système considéré et du coefficient de diffusion de J dans l’air (caractéristique physique qui peut varier avec la température). Nous n’entrerons pas davantage dans les détails à ce sujet. Un exemple de cette approche appliquée à la transpiration foliaire est donné au chapitre II.5. Disons simplement que lorsque le trajet comporte des tronçons successifs en série, chaque tronçon est caractérisé par une résistance particulière et la résistance du trajet complet est égale à la somme des résistances partielles. C’est le principe que nous adopterons pour décrire les échanges de CO₂ et H₂O de la feuille.

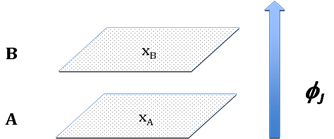
Figure 20. Diffusion gazeuse d’une substance J dans l’air. Le flux qui traverse les plans A et B est proportionnel à la différence de fraction molaire de J entre ces deux plans (voir texte).

·         Expression du flux de CO₂ absorbé par la feuille, profil de concentration du CO₂

Lorsque la photosynthèse est active, les chloroplastes constituent un puits pour le CO₂ dont les molécules diffusent depuis l’air entourant la feuille jusqu’aux cellules du mésophylle, avant de passer en phase liquide (dissolution) pour traverser les membranes cellulaires et atteindre les sites de carboxylation dans les chloroplastes. Le trajet en phase gazeuse traverse successivement la couche limite d’air, les ostioles stomatiques, les espaces aériens intercellulaires. Il s'effectue selon un gradient décroissant de concentration en CO₂ depuis l'air libre jusque dans l'espace poreux intra foliaire (parenchymes lacuneux et palissadiques) où la concentration devient très faible (figure 21).

Le flux net de CO₂ fixé par la feuille par unité de surface (assimilation nette, AN) s’écrit :

             (mol_CO2 m^-2 s^-1)                                                   (équat. 30)

avec

     : fraction molaire du CO₂ dans l’air ambiant, proche actuellement de 400 vpm 

 : fraction molaire du CO₂ en équilibre avec les chloroplastes au site de carboxylation[4]

      : résistance à la diffusion du CO₂ dans la couche limite

      : résistance stomatique (trajet diffusif à travers les ostioles et dans l’espace poreux mésophyllien)

      : résistance dite mésophyllienne (composante physiologique, biochimique, etc.)

·         Expression de la densité de flux d’eau transpirée :

En adoptant le même système de notation que pour l’assimilation nette, le flux de transpiration s’écrit :

                                  (mol_H2O m^-2 s^-1)                                   (équat. 31)

avec :

 : fraction molaire de la vapeur d’eau dans l’espace poreux interne de la feuille              

        : fraction molaire de la vapeur d’eau dans l’air ambiant

     : résistance à la diffusion de H₂O dans la couche limite

     : résistance stomatique (trajet diffusif à travers les ostioles et dans l’espace poreux mésophyllien)

Les résistances  et  impliquées dans la diffusion gazeuse des molécules d’eau diffèrent de celles concernant le CO₂. Le rapport r_H2O/r_CO2 est sensiblement égal à l’inverse du rapport des diffusivités de chacun des gaz dans l’air :

                     à 20°C                                                                   (équat. 32)

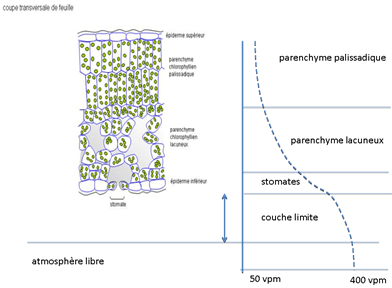
Figure 21. Coupe transversale de feuille et profil hypothétique de concentration (fraction molaire) de CO₂ entre l’atmosphère libre où elle est de 400 vpm et les sites de carboxylation où elle n’est plus que de 50 vpm environ (point de compensation pour le CO₂). Sur ce schéma on suppose que la baisse de concentration de CO₂ est principalement localisée au niveau des stomates. Autrement dit, la résistance stomatique est plus importante que les autres (Schéma de feuille tiré de BDS Secondaire- banque de schémas- > Biologie végétale, anatomie, croissance, développement...).

Pour la majorité des plantes adaptées à un climat tempéré et humide le fonctionnement foliaire est optimal tant que le potentiel hydrique (voir chapitre I.2) reste supérieur à -1,5 MPa. Dans ces conditions l'hygrométrie dans l'espace poreux interne de feuilles physiologiquement actives – c’est à dire l’humidité relative HR en équilibre avec le potentiel hydrique de la feuille (cf. équation 25, et figure 16 chapitre I.2) – est toujours très proche de la saturation : HR = 100%. Il en résulte que la pression partielle de vapeur d’eau dans l’atmosphère interne de la feuille est égale à , (cf. la fonction de vapeur saturante , chapitre I.2) c’est à dire qu’elle est uniquement fonction de la température de la feuille T_feuille. La fraction molaire de la vapeur d’eau dans les espaces poreux intra mésophylle devient alors .

L’air ambiant (en dehors de la couche limite) quant à lui est caractérisé par une pression partielle de vapeur d’eau p’. Par définition, la température de rosée Trosée  est la température pour laquelle p’ est saturante (apparition de rosée), ce qui permet d’écrire et pour la fraction molaire de vapeur d’eau dans l’air libre :   Finalement, le flux de transpiration s’écrit :

                                                                                           (équat. 33)

Le profil (hypothétique) de pression de vapeur à l’intérieur de la feuille est montré sur la figure 22.

On trouvera dans le complément C2 quelques indications sur le principe de mesure des résistances impliquées dans les équations ci-dessus.

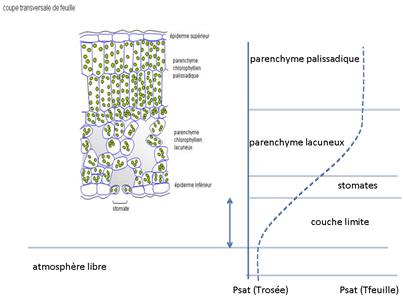
Figure 22. Profil hypothétique de pression de vapeur d’eau à l’intérieur de la feuille et dans la couche limite.  La vapeur d’eau est saturante à l’intérieur de la feuille.

C2 Principes de détermination des résistances FOLIAIRES

Résistance aérodynamique

La couche limite qui entoure les feuilles oppose une grande résistance aux transferts de chaleur ou de vapeur. Cette résistance, dite résistance aérodynamique foliaire, est fonction de la vitesse du vent mais aussi de la forme et de la rugosité des feuilles. On peut évaluer cette résistance en mesurant la température d’équilibre T_F de modèles physiques de feuille (mêmes forme et dimension) dans lesquels on dissipe par effet Joule un flux de chaleur constant f (W m^-2). La relation entre le flux de chaleur dissipé et l’écart de température T_F – T_a entre le modèle de feuille et l’air s’écrit :

                             (W m^-2)                                                                (équat. 34)

La résistance est la résistance aérodynamique de la couche limite pour la diffusion de la chaleur. On passe de  à

  ou   en multipliant par le rapport des diffusivités ou .

Résistance stomatique

La mesure de la résistance stomatique pour la diffusion de la vapeur d’eau peut se faire à l’aide d’un poromètre (cf. chapitre II.5). Il existe différents principes de poromètres mais il s’agit toujours de mesurer l’évaporation et la température d’une surface déterminée de feuille placée dans une petite enceinte parcourue par un courant d’air sec dont le débit est contrôlé. Connaissant la résistance aérodynamique, la résistance stomatique se déduit de l’équation 34.

Résistance totale

Le trajet couche limite – mésophylle est commun au CO₂ et à la vapeur d’eau et comprend deux résistances en série : la résistance aérodynamique et la résistance stomatique. La résistance à la diffusion de CO₂, est dans un rapport sensiblement constant avec la résistance r_H2O à la diffusion de vapeur d’eau (rapport des coefficients de diffusion moléculaire) :

r_CO2 = r_H2O . D_H2O/D_CO2 = 1,3 r_H2O                                                                  (équat. 35)

La photosynthèse est d’autant plus active que le transfert de CO₂ depuis l’air libre jusqu’à l'intérieur de la feuille est facile (r_CO2 faible). La régulation stomatique permet un ajustement de r_s dans de très grandes proportions, en fonction d’un grand nombre de paramètres dont notamment l’éclairement, le déficit de saturation de l’air, l’état hydrique du sol et des feuilles, etc. Remarquons que la condition r_CO2 faible implique r_H2O faible d’où l’étroite corrélation entre les intensités de la photosynthèse et de la transpiration.

Résistance mésophylienne

Une fois les résistances aérodynamique et stomatique connues à partir des mesures de transpiration, la composante mésophyllienne r_m qui caractérise le potentiel photosynthétique de la feuille doit être déterminée indépendamment à partir de mesures de photosynthèse.

C3       Cohésion de l’eau

On sait que l'eau possède une très grande cohésion mise en évidence dans certaines conditions de laboratoire.

La cohésion d'un liquide est la propriété selon laquelle on peut « tirer » sur une colonne du liquide sans la rompre. Normalement un liquide n'a pas de cohésion interne, ce qui veut dire que lorsqu'il est soumis à une pression inférieure à la pression de vapeur saturante il passe à l'état vapeur. Reportons-nous par exemple au diagramme des phases de l’eau (figure 5, chapitre I.2). Partons d’un état (T,P) situé dans la zone « liquide » et abaissons progressivement la pression. Le point se déplace verticalement vers le bas jusqu’à atteindre la courbe d’équilibre liquide-vapeur (courbe continue) au point de coordonnées T,   pour lequel normalement, l’eau entre en ébullition et tend à se vaporiser. C’est le phénomène de « cavitation » (formation de bulles au sein du liquide). Ce phénomène explique par exemple que l'on ne peut aspirer de l'eau au delà d'une hauteur d'environ 10 mètres à l'aide d'une pompe aspirante, ou que la colonne de mercure retournée sur la cuve à mercure se stabilise à une hauteur correspondant à la pression atmosphérique (principe du baromètre à mercure).

De multiples expériences démontrent toutefois que l'eau peut rester à l'état liquide même lorsqu'elle est soumise à des tensions extrêmement élevées. C'est le cas par exemple des expériences de Berthelot (1850) où des échantillons d'eau enfermés dans des ampoules de verre scellées et fortement refroidies restent liquides alors que les pressions internes calculées sont de l'ordre de -50 bars (-5 MPa), impliquant normalement le passage à l’état vapeur. Il en va de même dans les inclusions liquides au sein de minéraux, où l'état liquide subsiste alors que le calcul indique des tensions de l'ordre de -100 MPa (El Mekki-Azouzi, 2010).

Dans toutes ces expériences l’eau est dans un état métastable qui normalement prend fin instantanément et brutalement (phénomène de cavitation) sous l'effet de chocs, vibrations, présence de bulles, etc. De façon moins exotique, l'eau dans un sol non saturé est un exemple classique de ces états où l’eau resterait liquide (du point de vue de l’organisation des molécules entre elles, il s’agit peut-être d’un état proche du solide) bien que se trouvant à des pressions négatives quelquefois très basses. Dans ce dernier cas, le phénomène s'expliquerait par des interactions électriques entre l'eau et les particules du sol. La seule considération de la pression et de la température n'est donc pas un critère suffisant pour affirmer que l'eau se trouve ou pas à l'état liquide. Il faut en outre faire intervenir les conditions physico-chimiques du milieu à l'échelle moléculaire. Encore s'agit-il d'un domaine très peu documenté.

La cohésion de l'eau est un des effets des liaisons « hydrogène » qui s'établissent statistiquement entre l'atome O d'une molécule H₂O et les atomes H des 2 à 4 molécules voisines, du fait du caractère polaire de la molécule H₂O. En effet, même à l'état liquide les molécules d'eau ne sont pas indépendantes les unes des autres; elles sont soumises à des forces de liaison électrostatiques qui tendent à les rapprocher. Ces liaisons hydrogène, bien qu'extrêmement labiles (durée de vie de l'ordre de 10^-12s) confèrent à l'eau des propriétés extraordinaires par rapport à d'autres liquides: valeurs extrêmement élevées de capacité calorifique, chaleur latente de vaporisation, tension superficielle, cohésion.

La cohésion de l'eau est fondamentale pour comprendre comment la sève des plantes peut monter à des hauteurs nettement supérieures aux 10 mètres fatidiques qui correspondent à la pression atmosphérique et atteindre le sommet des plus grands arbres (>100m). Le calcul montre en effet que dans bien des cas, particulièrement celui des grands arbres, la pression à laquelle est soumise la sève dans les vaisseaux proches des feuilles transpirantes peut atteindre des valeurs négatives extrêmement basses, de l'ordre de -1 à -10 MPa par exemple.

La cohésion particulièrement élevée de l'eau explique sans doute la possibilité d’observer chez les plantes, de tels états très éloignés de l'équilibre. Remarquons cependant que pour les observer en laboratoire, il faut prendre des précautions expérimentales peu ordinaires (grande pureté de l'eau, absence de germes et de gaz dissous,...). Il faut donc admettre qu’un mécanisme encore largement inexpliqué protège les plantes de la cavitation, et en limite les conséquences désastreuses pour la fonction conductrice du xylème (embolie). On sait que des mécanismes physiologiques actifs sont à l’œuvre pour réparer pendant la phase nocturne les aptitudes conductrices des vaisseaux embolisés en cours de journée, mais il faut probablement admettre que des propriétés physico-chimiques particulières des paroi ou encore d’autres mécanismes physiologiques sont impliqués dans le fait que l’embolie des vaisseaux reste malgré tout un phénomène en général assez limité.