Le sol, milieu de diffusion de l’eau liquide

 

Au cours de l’année, les sols, en particulier dans leurs horizons supérieurs, subissent des alternances d’humectation et de dessiccation, principalement dans leurs horizons supérieurs. Celles-ci sont plus ou moins longues selon qu’elles correspondent à des rythmes saisonniers ou à des successions de périodes sèches puis pluvieuses. Il en résulte des profils d’humidité dans le sol très variables dans le temps et l’espace, selon que le sol est nu ou cultivé, et que l’on se trouve en période pluvieuse ou non. Ces variations d’humidité impliquent des transferts hydriques contribuant, soit à recharger le sol, soit au contraire à le vider partiellement de son eau. La réhumectation du profil du sol se fait par infiltration de l’eau de pluie ou d’irrigation ; elle peut aussi résulter, mais généralement dans une moindre mesure, de remontées capillaires à partir de la nappe phréatique ou de couches humides du sous-sol. Le dessèchement est la conséquence de l’absorption de l’eau par les plantes et/ou de l’évaporation de l’eau du sol vers l’atmosphère (la somme de ces deux flux constituant l’évapotranspiration).

Dans un sol, l’eau n’est donc pas immobile : elle se déplace constamment, plus ou moins vite, d’un point à un autre et dans toutes les directions (pas seulement dans le sens vertical comme on a pourtant tendance à le penser). Ces déplacements sont toujours sous la dépendance de différences de potentiel hydrique. L’eau étant un solvant, ses mouvements s’accompagnent de celui des solutés qu’elle transporte (sels dissous, pesticides, …), mais aussi des particules en suspension et des organismes microbiens. Cela peut conduire à des risques de pollution pour les eaux profondes et/ou à l’accumulation de sels en surface.

L’étude physique des transferts d’eau dans le sol distingue en général deux grands domaines : celui des sols saturés et celui des sols non saturés. Dans les deux cas le flux d’eau qui circule entre deux points est égal au gradient de potentiel hydrique multiplié par un coefficient appelé conductivité hydraulique. Toutefois, alors que dans un sol saturé la conductivité hydraulique ne varie pas car la teneur en eau ne varie pas (seule la pression peut varier), il n’en va pas du tout de même dans un sol non saturé car les mouvements d’eau s’y accompagnent de variations concomitantes de teneur en eau, potentiel hydrique et conductivité hydraulique. De ce fait, l’expression des mouvements d’eau dans un sol non saturé fait appel à un formalisme différentiel beaucoup plus compliqué. Nous n’en donnerons ici qu’un bref aperçu.

 

IV.1 Flux d’eau dans un sol saturé : loi de Darcy.

Lorsque le sol est saturé, tous les pores sont remplis d’eau, il n’y a pas de phase gazeuse et la phase liquide est continue. Les forces de capillarité disparaissent dès lors que la composante matricielle du potentiel hydrique est nulle ou négligeable. L’eau s’écoule dans tous les pores qui sont interconnectés, mais ce sont les plus gros qui assurent l’essentiel du flux en masse. On parle d’infiltration lorsque l’écoulement s’effectue verticalement sous l’effet de la gravité. Les vitesses d’infiltration sont généralement comprises entre 0,1 et 10 cm par heure.

Les lois des écoulements en sol saturé ont été établies à l’aide d’expériences du type de celle représentée figure 24. L’échantillon de sol saturé est disposé dans un cylindre de section S et de longueur L dont les extrémités A et B sont reliées à des récipients à niveau constant R1 et R2 respectivement. On mesure le débit Q (m³ s^-1) d’eau qui s’écoule en fonction de la différence d’altitude DZ entre les deux récipients.

Remarquons que dans un tel dispositif, il n’y a pas d’écoulement si les récipients R1 et R2 sont au même niveau (vases communicants), bien que les pressions en A et en B soient différentes (du fait de l’inclinaison du cylindre). Si P désigne la pression hydrostatique en tout point et z l’altitude, on sait que la condition d’équilibre hydrostatique d’un fluide incompressible (absence de mouvement, donc débit nul) peut s’écrire :

rgz + P = constante                                                                                       équation 20

Remarquons que cette expression n’est autre que celle du potentiel hydrique total puisque, s’agissant d’un sol saturé, les seules composantes qui interviennent sont la composante de pression (Y_p=P) et la composante gravitationnelle (Y_g=rgz). Nous venons donc de vérifier que l’équilibre hydrostatique dans un sol saturé correspond à l’uniformité du potentiel hydrique total, ce qui n’est pas étonnant.

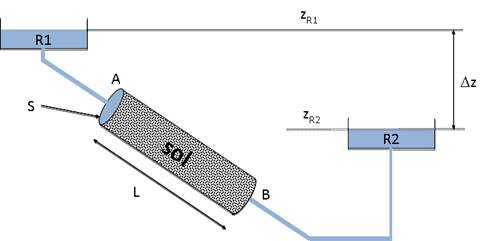
Figure 24. Dispositif schématique illustrant la loi de Darcy. Une colonne de sol saturée AB inclinée est traversée par un débit d’eau sous l’effet de la différence de niveau Dz (m) entre les réservoirs R1 et R2. La loi de Darcy indique que le débit d’eau à travers la colonne de sol est proportionnel à la section S et à Dz et inversement proportionnelle à la longueur de la colonne L. La hauteur Dz est ce qu’on appelle la perte de charge ; elle représente en termes de hauteur d’eau la chute de potentiel hydrique (DY = rgDz) entre A et B. Ce dispositif permet de définir et de mesurer la conductivité hydraulique à saturation du sol, K_H (m s^-1).

Explicitons la différence de potentiel hydrique entre les points A et B d’altitude z_A et z_B respectivement. Comme nous venons de le voir, le potentiel total en tout point peut s’écrire :

Y_total = rgz + P

La pression en A est due à la colonne d’eau de hauteur z_R1-z_A située au dessus de A. La composante hydrostatique (exprimée en pression relative, c’est à dire en écart par rapport à la pression atmosphérique) est donc donnée par rg (z_R1-z_A). D’où l’expression du potentiel total en A :

Y_{total A} = rgz_A + rg (z_R1 - z_A) = rg z_R1

Nous trouvons de même pour le point B :

Y_{total B} = rgz_B + rg (z_R2 – z_B) = rg z_R2

Remarquons en passant que les altitudes z_A et z_B n’interviennent pas dans l’expression du potentiel hydrique en A et B. Seules comptent les altitudes des récipients R1 et R2.

Si Y_B est plus faible que Y_A, il s’établit un flux d’eau de A vers B. L’expérience montre que Q est

-         proportionnel à la section du cylindre S (m²),

-         proportionnel à la différence d’altitude Dz entre les deux récipients (Dz=z_R1 – z_R2)  (m),

-         inversement proportionnel à la longueur L du cylindre, soit :

                                                                                 équation 21

Le coefficient de proportionnalité K_H s’appelle la conductivité hydraulique à saturation du sol et elle s’exprime en m s^‑1. Les mesures montrent que le sable laisse passer un débit 100 000 fois plus important que l’argile. Les flux sont dans le rapport de leurs conductivités hydrauliques à saturation K_H.

Note : par convention, le débit Q sera positif si l‘eau coule de A vers B, il sera négatif dans le cas contraire, l’eau circulant dans le sens des potentiels décroissants. Si l’on réécrit  l’équation ci-dessus en introduisant les potentiels hydriques. Il vient :

                (m³ s^-1)                                                 équation 22

On voit que cette expression, qui est positive, respecte bien la convention de signe retenue puisque l’eau circule de A vers B si Y_A >  Y_B

Raisonnons maintenant de façon plus générale en termes de différences finies dans une direction. Partant de A et allant vers B, notre abscisse s’accroît de Dx que le potentiel hydrique subit un accroissement DY = Y_B - Y_A. On voit alors que la façon correcte d’exprimer le débit Q en respectant la convention de signe est :

                                                                                         équation 23

Le signe – qui apparaît désormais dans l’équation de Darcy est simplement la traduction algébrique du fait que l’eau s‘écoule dans le sens des potentiels décroissants. Nous nous attacherons à respecter cette convention dans la suite de ce chapitre.

 

Formes différentielle et vectorielle de la loi de Darcy

Exprimons la grandeur j = Q/S que l’on appelle densité de flux et qui s’exprime en m s^-1. Cela va nous permettre de considérer directement un tube de section dS arbitrairement petite. La loi de Darcy prend alors la forme suivante que nous adopterons désormais :

               (m s^-1)  

Isolons par la pensée à l’intérieur de la colonne précédente d’axe orienté Ox quelconque (Fig. 25), un tube élémentaire de section dS et plaçons nous à l’abscisse x. Considérons un accroissement dx arbitrairement petit auquel correspond une petite variation de potentiel total dY  et exprimons la densité de flux d’eau j qui traverse la surface élémentaire dS nous obtenons la loi de Darcy sous sa forme différentielle :

                               (m s^-1)                                  équation 24

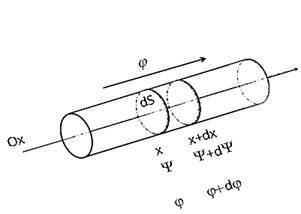
Figure 25. Forme différentielle de la loi de Darcy. On exprime ici le flux d’eau dans un tube élémentaire orienté d’axe Ox et de section dS situé au sein de la colonne de sol saturé. On considère pour cela un déplacement arbitrairement petit dx (voir texte).

Remarque : en sciences de l’hydraulique, la notion de potentiel hydrique est remplacée par la charge hydraulique h qui correspond à la hauteur d’eau équivalente au potentiel hydrique. La loi de Darcy prend alors la forme particulièrement simple :

On démontre par ailleurs que cette loi est aussi valide vectoriellement, soit :

    ou encore :                                       équation 25

N.B. c’est sous cette forme vectorielle que la loi de Darcy permet d’aborder numériquement les problèmes de circulation de l’eau en milieu poreux saturé avec les géométries les plus complexes.

 

Conductivité hydraulique à saturation de différents types de sols

D’une façon générale, la conductivité d’un sol saturé varie de plusieurs ordres de grandeur principalement selon la texture (Fig. 26). Les sols les plus perméables (pour lesquels K_H a les valeurs les plus grandes) sont les sols sableux dans lesquels des pores larges et en continuité les uns avec les autres, constituent l’essentiel de la porosité, les moins perméables les sols argileux fortement humectés dans lesquels la circulation de l’eau se fait surtout dans des micropores. Ceci explique pourquoi les mouvements de l’eau sont bien plus rapides dans les sols sableux saturés que dans les sols argileux saturés. Il en va tout autrement dans le domaine non saturé (voir plus loin).

 

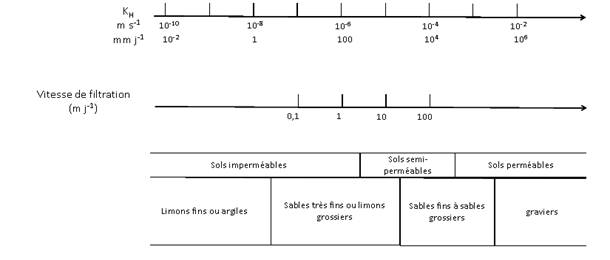
Figure 26. Conductivité hydraulique à saturation de différents types de sols. Sa gamme est extrêmement étendue (5 ou 6 ordres de grandeur selon la texture). La conductivité hydraulique à saturation à la surface du sol est un des éléments déterminants de la vitesse d’infiltration mais elle n’est pas le seul. Interviennent entre autre les propriétés des couches sous-jacentes (conductivité, potentiel hydrique).

 

Remarque : analogie entre loi de Darcy et loi d’Ohm (analogie électrique)

Il existe une analogie formelle entre la loi de Darcy  et la loi d’Ohm  qui exprime l’intensité I d’un courant électrique qui parcourt une résistance R sous l’effet d’une différence de potentiel électrique V_A - V_B. Dans ces deux lois le flux est orienté dans le sens des potentiels (Y ou V) décroissants, son intensité (Q ou I) est proportionnelle à la différence de potentiel et elle est inversement proportionnelle à une résistance. La résistance électrique R s’exprime en ohms et on sait qu’elle peut aussi s’écrire :

où r_e désigne la résistivité électrique du matériau constitutif de la résistance, l sa longueur et S sa section.

Dans la loi de Darcy, l’expression   joue exactement le même rôle que R en électricité ; elle définit ce que l’on l’appelle souvent la résistance hydraulique du trajet AB. On voit aussi que le rapport rg/K_H est l’analogue de la résistivité électrique.

L’analogie entre les deux lois repose en fait sur une certaine communauté de nature entre les deux phénomènes. Du point de vue thermodynamique il s’agit dans les deux cas de phénomènes dissipatifs, c’est à dire dans lesquels une différence de potentiel (niveau d’énergie) a tendance à se dissiper spontanément sous forme de chaleur du fait notamment des frottements. Il s’agit d’un type de phénomènes extrêmement répandus dans la nature et pour lesquels en première approximation, le taux de dissipation est proportionnel au gradient de potentiel, ce qui débouche sur des lois macroscopiques formellement très proches. Cette analogie électrique est utilisée dans de nombreux domaines notamment dans celui du fonctionnement hydraulique des plantes (voir Chap. II.6). Un des intérêts de cette analogie est qu’elle autorise une certaine transposition des méthodes de calcul et de modes de raisonnement développés en électricité à ces autres domaines. Nous verrons comment ces remarques s’appliquent au domaine des relations plantes/eau, en particulier au domaine du sol non saturé (§  IV.2) et à la plante.

 

IV.2 Flux d’eau dans un sol non saturé

Lorsque le sol n’est pas saturé, l’eau n’occupe pas tout l’espace poral, ce qui a au moins trois conséquences importantes :

1- la teneur en eau n’est plus constante, que ce soit dans l’espace ou dans le temps,

2-les phénomènes de capillarité deviennent de plus en plus importants au fur et à mesure que le sol se dessèche, ce qui veut dire aussi que la composante matricielle Y_m du potentiel hydrique devient rapidement dominante par rapport à la composante gravitationnelle Y_g. Autrement dit, la pesanteur joue beaucoup moins, voire pas du tout, sur les mouvements d’eau que dans le domaine saturé.

3- la conductivité hydraulique K_H chute fortement, car ce sont les pores les plus gros qui se vident les premiers alors qu’ils participent le plus à la circulation de l’eau. Seuls les petits pores assurent alors les voies de circulation de l’eau.

Autant l’état de saturation du sol est relativement bien défini et facile à caractériser en termes de teneur en eau volumique H_v, ou de conductivité hydraulique K_H, autant lorsqu’on aborde le domaine du sol non saturé, il faut réaliser que tous les paramètres hydrodynamiques sont susceptibles de varier de plusieurs ordres de grandeur en fonction les uns des autres, dans l’espace et au cours du temps. Il en résulte entre autre que les calculs dans ce domaine deviennent vite très complexes et susceptibles d’erreurs importantes dans la mesure où les fonctions qui décrivent ces variations, Y_m(H_v) ou K_H(Y_m) par exemple, sont assez mal connues par suite de difficultés expérimentales et méthodologiques.

 

Loi de Darcy généralisée

Nous avons schématisé (Fig. 24) le dispositif expérimental simple utilisé par Darcy pour mesurer la conductivité hydraulique à saturation. Pour diverses raisons, on ne peut pas utiliser un dispositif aussi simple pour établir une loi de circulation de l’eau en sol non saturé et en mesurer la conductivité hydraulique. On admet donc généralement a priori la validité de la loi de Darcy en milieu non saturé sous sa forme vectorielle tout en faisant apparaître comme condition supplémentaire que la conductivité est une fonction du potentiel matriciel :

                                                     équation 26

Sous cette forme il s’agit de l’équation dite de Darcy généralisée. L’extension au domaine non saturé de la proportionnalité entre flux d’eau et gradient de potentiel matriciel ne pose pas de problème de principe ; des considérations théoriques permettent de la justifier comme pour le domaine saturé. La loi de Darcy généralisée peut s’appliquer à différentes échelles et à des géométries 3D. C’est ainsi qu’on peut la trouver utilisée pour décrire les flux d’eau au voisinage de racines en géométrie cylindrique (Lambert et Penning de Vries, 1973).

La validité de l’équation de Darcy généralisée étant admise, la difficulté n’en reste pas moins qu’il convient concrètement de mesurer la conductivité hydraulique sur toute une gamme d’humidité ou de potentiel matriciel et à différents endroits dans une parcelle (échantillonnage) pour essayer de rendre compte des hétérogénéités du terrain. Des techniques de terrain et de laboratoire existent qui toutes restent assez complexes ou lourdes à mettre en œuvre.

La compilation des résultats obtenus par différents auteurs confirme la vaste gamme de variation de K_H et des comportements en fonction de la texture. La figure 27 montre un exemple du comportement de K_H en fonction de la variation du potentiel matriciel du sol pour un sol argileux et un sol sableux. On constate sur cette figure que pour les deux types de sol la conductivité hydraulique présente une croissance quasi exponentielle avec la teneur en eau (ou le potentiel matriciel), la valeur maximale étant observée lorsque le sol est saturé ; que par ailleurs les deux courbes se croisent. Ainsi, le sol sableux qui présente la conductivité hydraulique la plus élevée à saturation (du fait de la dimension importante des pores), devient presque imperméable lorsque le potentiel devient inférieur à -10 kPa alors que le sol argileux au même potentiel hydrique, conserve une certaine aptitude aux transferts d’eau du fait de la microporosité.

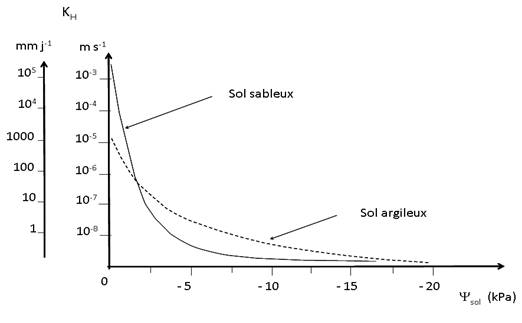
Figure 27. Variation de la conductivité hydraulique non saturée K_H en fonction du potentiel matriciel, pour un sol sableux et un sol argileux. K_H varie considérablement au voisinage de la saturation, en particulier pour le sol sableux. Les deux courbes se croisent vers 2 kPa. Pour des potentiels matriciels plus faibles la conductivité hydraulique du sol argileux devient supérieure à celle du sol sableux. D’après Musy et Soutter, 1991.

Une fois déterminées expérimentalement les variations de K_H en fonction de Y, des ajustements mathématiques non-linéaires permettent de les introduire dans des modèles numériques de transfert. Une des approches consiste à utiliser une forme paramétrique de la loi de variation de la conductivité hydraulique en fonction de l’humidité ou du potentiel hydrique, par exemple sous la forme K_H = aY^b, a et b étant deux constantes numériques.

Malgré la gamme très étendue des variations du coefficient Kh, la loi de Darcy est utilisée par les physiciens du sol, pour prédire l’évolution de ta teneur en eau, au moyen d’une loi de conservation classique, appelée loi de Richards. Ceci déborde du cadre de ce chapitre et on trouvera dans les ouvrages spécialisés (Calvet 2003, Kirkham, 2004) des développements approfondis sur le transport de l’eau en milieu insaturé.