Bilan radiatif et bilan énergétique de la feuille

La feuille absorbe le rayonnement solaire, de façon variable selon la longueur d’onde. La figure 6 représente de bas en haut la fraction de rayonnement réfléchie par la feuille (en bleu) et de haut en bas la fraction de rayonnement transmise par la feuille (en rouge), en fonction de la longueur d'onde. La zone entre les deux courbes représente la fraction absorbée par la feuille. Dans le domaine visible (0,4 à 0,7 µm), les pigments photosynthétiques (chlorophylles, caroténoïdes et xanthophylles) absorbent fortement (coefficient d’absorption α = 0,85 en moyenne) tandis que dans le proche infrarouge (0,7 à 4 µm), l’absorption est beaucoup plus faible (α = 0,25 en moyenne). Comme le visible et le proche infrarouge sont en part presque égales dans le spectre solaire à la surface terrestre, α vaut en moyenne environ 0,55 pour l’ensemble du rayonnement solaire R_g (rayonnement global). Le rayonnement absorbé est dissipé de plusieurs façons :

-          la feuille émet un rayonnement infrarouge de grandes longueurs d’onde (4 à 50 µm) et en reçoit également du sol et du ciel.

-          elle échange de la chaleur avec l’air par diffusion et convection du fait de sa température différente de celle de l’air (chaleur dite sensible)

-          elle se refroidit en évaporant l’eau transpirée (chaleur latente)

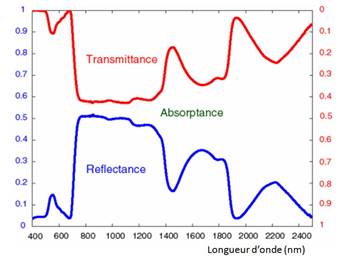
Figure 6. Propriétés optiques d'une feuille verte

On appelle R_n le rayonnement net de la feuille. On peut en avoir une bonne approximation avec l’expression suivante pour une feuille horizontale qui reçoit le rayonnement atmosphérique R_a sur sa face supérieure, le rayonnement émis par le sol ε_sσT_s⁴ sur sa face inférieure, et émet le rayonnement ε_f σT_a⁴ par ses deux faces :

            R_n = α.R_g. (1+a) +ε_f.(R_a – σT_a⁴) + ε_f.( ε_sσT_s⁴ - σT_a⁴)

où α peut être pris égal à 0,55, a albédo[9] de la surface sous la feuille est de l’ordre de 0,2. ε_f et ε_s émissivités de la feuille et du sol (égale au coefficient d’absorption dans l’infrarouge lointain, environ 0,95). R_a est le rayonnement infrarouge de l’atmosphère et σT_a⁴ est le rayonnement émis par la feuille en assimilant ici encore T_f à T_a, avec σ constante de Stefan-Boltzmann égale à 5,67.10^-8 W m^-2 K^-4. Le terme ε_sσT_s⁴ - σT_a⁴ est souvent négligé, les températures étant proches, surtout quand s se rapporte à la surface de la feuille sous-jacente.

Le bilan énergétique de la feuille s’écrit en égalant le rayonnement net à la somme de la chaleur sensible H et de la chaleur latente λE émises par les deux faces de la feuille:

            R_n = H + λE                                                                                                                               (4)

où H =2.(ρc_p/r_a).(T_f – Ta)                                                                                                                   (5)[10]

λE peut aussi être exprimée à l’aide de (3) :  

            λE = 2.λ.(M_e/RT_a). (e_s(T_f) - e_a)/ (r_s + r_a),

qu’on peut simplifier en introduisant la constante psychrométrique[11]       γ = ρc_p.RT_a/(λ.M_e),en

            λE = 2.(ρc_p/ γ). (e_s(T_f) - e_a)/ (r_s + r_a)                                                                                       (6)