Quelques notions de base et exemples clefs

Définition et ordre de grandeur

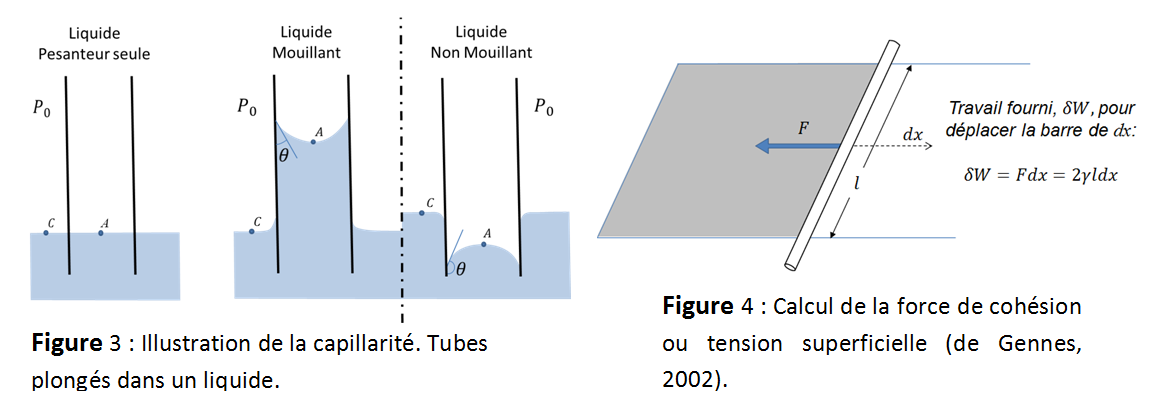
La capillarité est l’étude des interfaces entre deux liquides non miscibles ou entre un liquide et l’air. Elle est présente dans de nombreuses situations du quotidien. Pour l’illustrer il suffit de regarder le comportement des liquides dans des tubes (Figure 3). Un liquide soumis aux seules forces de la pesanteur, c'est-à-dire à son poids, arriverait dans le tube à la même hauteur que celle dans le récipient qui le contient. Il serait également limité à l'interface avec l'air par une surface plane et horizontale. Cette observation peut s'expliquer par les lois de la statique des fluides à condition de supposer que le liquide n'est soumis qu'aux seules forces de pesanteur. Or, si l'on examine la surface libre à l'intérieur des tubes, le liquide n’est pas au même niveau que dans le récipient et on ne retrouve pas une surface plane et horizontale (on parle de ménisque). On peut montrer que ces phénomènes s'expliquent par l'action d'autres forces que celles de la pesanteur: des forces d'origine moléculaire. Les attractions entre molécules de la même espèce à l'état liquide, comme par exemple les attractions eau-eau dues aux liaisons hydrogène, s'appellent cohésion (Cf. Chap. I.1). L'attraction entre des molécules d'espèces différentes, comme celle qui a lieu entre un liquide et une phase solide telle une paroi de capillaire ou la surface d'une feuille, s'appelle adhésion. Lorsque les forces impliquées dans l'adhésion liquide-paroi sont importantes comparées à celles en jeu dans la cohésion entre les molécules du liquide, le liquide est dit mouillant et un film d'eau plus ou moins étendu remonte le long les parois. Dans le cas d'un récipient contenant de l'eau, cela signifie que l'interface eau-paroi est située au-dessus du plan de l'eau loin des parois. A l'opposé, quand les forces de cohésion à l'intérieur d'un liquide sont grandes devant les forces d'adhésion entre le liquide et la paroi, le liquide est dit non mouillant et l'interface liquide-paroi est à un niveau inférieur à celui du liquide loin de la paroi. C'est par exemple ce qui se passe avec le mercure. Ce comportement est explicité dans le paragraphe « Equilibre des pressions et Loi de Laplace ». La force mise en jeu est dénommée force capillaire, ou plus communément tension superficielle. Elle est généralement notée g.

Pour estimer l’intensité de la tension superficielle, il faut mesurer la force d’attraction des molécules entre elles en présence d’une interface. Pour l’illustrer, considérons un système simple et couramment utilisé composé d’un film liquide dans un cadre rectangulaire dont un des côtés peut se déplacer (Figure 4). La force à imposer pour déplacer la barre d’une distance dx et augmenter ainsi la surface du film, va contrebalancer les forces de cohésion qui tendent à ramener la surface libre à son état initial. Il est alors possible de montrer que la force exercée est normale à la barre et proportionnelle à la longueur de la tige. La tension superficielle g est alors définie comme une force par unité de longueur dirigée vers le liquide et s’exprime en N.m^-1. La tension superficielle peut aussi se définir comme une énergie à fournir pour augmenter une surface d’une unité, g s’exprime alors en J.m^-2 (de Gennes, 2002). Les deux visions : énergie ou force, représentent deux facettes du même phénomène et, selon le système étudié, l’une ou l’autre de ces formulations sera utilisée pour faciliter le raisonnement.

La tension superficielle peut fortement varier d’un liquide à l’autre en fonction de sa composition (pur, mélange, présence de surfactant) et de sa température (de Gennes, 2002). Par exemple, l’élévation de la température tend à diminuer la tension superficielle d’un liquide. Le tableau 1, regroupe quelques valeurs de tension superficielle à l’interface liquide/air et à température ambiante (20°C). Une liste plus exhaustive peut être trouvée dans de nombreux ouvrages ou sites dédiés (Broch, 2016 ; Christensen-Dalsgaard et al., 2011; de Gennes, 2002).

Tableau 1. Tension superficielle de quelques interfaces liquide/air ou liquide/liquide.

Mouillage

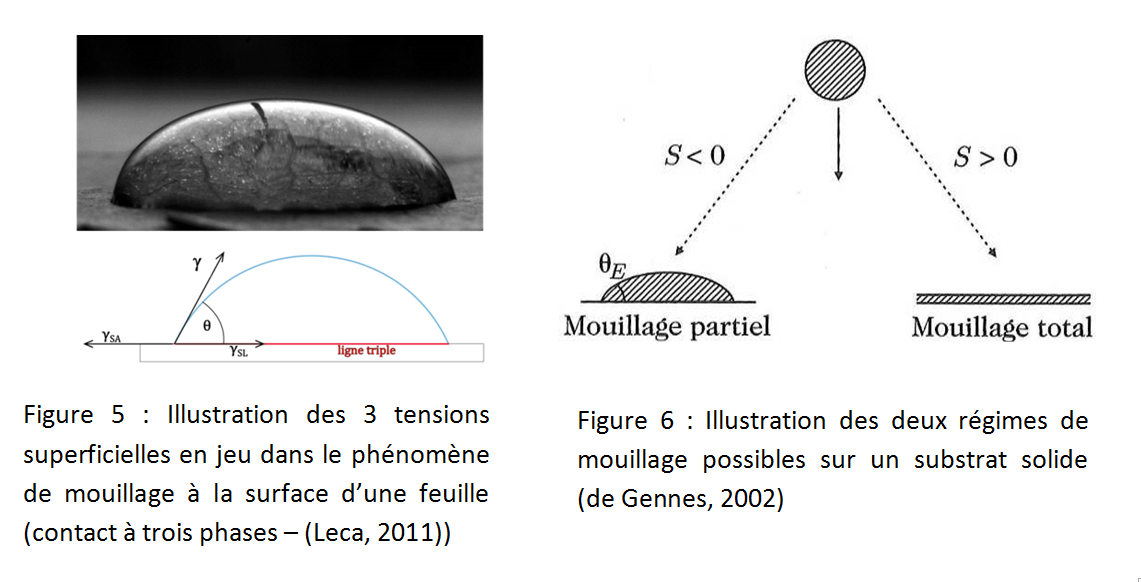
Pour illustrer le rôle primordial de la tension superficielle, reprenons le cas d’une goutte qui s’étale naturellement sur une feuille (figure 1) ou le cas du ménisque qui se forme naturellement près de la paroi d’un tube (figure 3). Dans ces cas il s’agit d’une interphase triple qui met en jeu un liquide, l’air et un substrat. Trois forces capillaires sont en jeu : la force liquide/substrat, g_SL, la force substrat/air, g_SA, et la force liquide/air,  g  (figure 5).

Aux bords de la goutte ces trois tensions vont s'exercer en compétition. La différence entre les tensions du substrat sec et mouillé permet de définir le paramètre d'étalement noté S qui rendra compte du mouillage du liquide sur le substrat, soit :

              en J.m^-2                     Eq. 1

Ainsi, si S est positif, la tension superficielle à l'interface solide/air l'emporte et la goutte s'étale complètement sur le substrat : on parle de mouillage total (Figure 6). Si au contraire S est négatif, la goutte ne s'étale pas complètement et va s'équilibrer sous la forme d'une calotte sphéroïde : on parle de mouillage partiel (Figure 6).

L'angle formé entre le bord de la goutte et le substrat est appelé angle de Young ou angle de contact, noté θ. L'angle de contact est délimité par les tensions interfaciales à la ligne triple (ensemble des points où l'interface est triple : air-liquide-solide, on pourrait également parler des bornes extérieures de la surface de contact entre la goutte et le support).

En équilibrant (la goutte a donc fini de s'étaler !) ces 3 forces capillaires le long du support (ou « ligne triple ») on obtient la relation de Young (1805) :

                                                Eq. 2

Cette relation définit l’angle de contact, q, en fonction des propriétés des 3 éléments présents. On peut également écrire cet équilibre en fonction du paramètre d'étalement S :

                                                        Eq. 3

Hydrophobie/hydrophilie et angle de contact

Si, à un substrat donné, l'étude du mouillage d'un liquide donne la grandeur de son étalement sur ce matériau, l'étude de la mouillabilité du substrat permet de caractériser son caractère hydrophile ou hydrophobe, c’est-à-dire sa tendance à favoriser ou non l’étalement d’une goutte de tout liquide.

Ainsi, un support hydrophile va avoir tendance à minimiser l'écart entre g_SA et (g_SL + g), alors qu'un support hydrophobe aura tendance à augmenter cet écart. La conséquence se répercute sur l'angle de contact. Ainsi, plus le paramètre d'étalement est petit, plus le cosinus de l'angle de contact sera grand :

                                                                  Eq. 4

La connaissance de l'angle de contact nous donne donc des informations sur l'hydrophobie du substrat (Zisman, 1964). Selon l'application, on recherche soit un mouillage optimal, soit une grande hydrophobie des matériaux. Il n’existe pas d’indicateur universel de la "qualité" d'hydrophobie. Les matériaux sont alors décrits en fonction de leur hydrophilie/hydrophobie, sous les termes : superhydrophile si θ<40°, hydrophile si θ <90°,  plutôt hydrophobe si 90°< θ <120°, hydrophobe si 120°< θ <150° (il arrive qu'on ne distingue pas les cas plutôt hydrophobe et hydrophobe), et superhydrophobe si θ>150° (Bhushan and Jung, 2008) (Figure 7).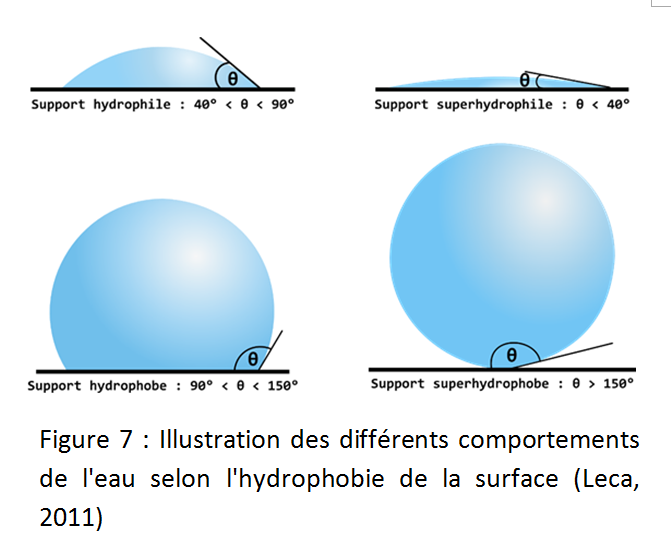

En termes de mouillabilité (wettability), on parlera de substrat mouillable (wettable) si θ < 110°, et de substrat non mouillable (non-wettable) si θ > 110° (Aryal and Neuner, 2010).

Angles de contact dynamiques et hystérésis

Dans la nature, l’apparition ou la disparition des gouttes est un processus dynamique. Par exemple, lors d’un épisode de rosée, des gouttes d’eau vont apparaître sur les feuilles et leurs tailles vont augmenter au cours du temps. Cette augmentation va induire un mouvement du liquide à la surface de la feuille. Ce mouvement ne pourra se faire qu’à partir d’un certain angle de contact appelé angle d’avancée, θ_a. Le phénomène inverse se produit lorsqu’une goutte va s’évaporer. La disparition du liquide induit une diminution de la taille de la goutte et un retrait de sa surface de contact sur la feuille. Ce retrait ne peut se faire qu’à partir d’un angle seuil appelé angle de recul, θ_r.

Ainsi, et en règle générale, la mobilité des gouttes en contact avec un substrat est décrite à l’aide de ces 2 angles de contact appelés angles dynamiques, dont la différence est appelée hystérésis d’angle de contact :. Ces deux angles correspondent aux angles limites que peuvent prendre une goutte sur un support. Ainsi l’angle d’une goutte à l’équilibre, θ, sera toujours compris entre les angles de recul, θ_r, et d’avancé, θ_a.

Il existe différentes méthodes expérimentales pour déterminer ces angles, nous en présenterons ici deux qui permettent de bien illustrer les phénomènes naturels de mouillage d’une feuille : la méthode du plan incliné et celle du gonflage/dégonflage.

Le plan incliné - La première méthode consiste à disposer une goutte du liquide considéré sur le substrat étudié, dont on peut augmenter graduellement l’inclinaison. A l’instant critique où la goutte entre en mouvement, elle présente les angles de contact propres au système goutte-substrat : on appelle l’angle le plus grand (au bas de la pente) l’angle d’avancée θ_a, et l’angle le plus petit (en haut de la pente) l’angle de recul θ_r.

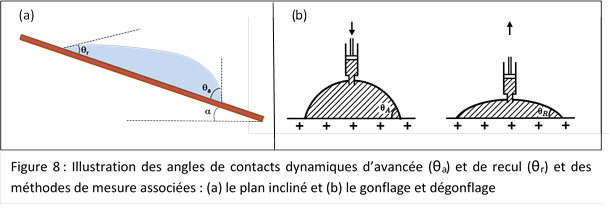Le gonflage/dégonflage - La seconde méthode présentée consiste à gonfler progressivement une goutte de liquide sur le substrat étudié. Dans un premier temps, la goutte va grossir avec une surface de contact liquide-substrat constante. A l’instant critique où cette surface se met à augmenter, l’angle de contact de la goutte est l’angle d’avancée θ_a. De manière similaire, en aspirant la goutte sur le substrat, on détermine l’angle de contact de recul θ_r à l’instant où la surface liquide-substrat commence à diminuer.

Equilibre des pressions et Loi de Laplace

Les observations montrent que les forces de tension superficielle sont orientées vers le liquide (Figure 4). Cela conduit à un phénomène largement connu sous le nom de « discontinuité de pression » et qui se formalise par le théorème de Laplace qui régit la discontinuité de pression à l’interface d’une surface (de Gennes, 2002).

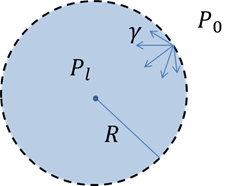
Figure 10 : Gouttelette d’eau dans l’air : illustrations des grandeurs intervenant dans la Loi de Laplace.

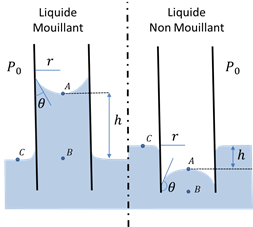
Figure 11: Discontinuité de pression ménisque liquide-air (Cours Mécanique des Fluides - Pr. H. Broch)

Pour illustrer ce phénomène, raisonnons sur le cas d’une goutte sphérique (figure 10). La tension de surface induit une force vers le liquide (Figure 3). Ainsi les forces de tension tendent à ramener le liquide sur lui-même et donc à la comprimer. Cette compression induit une surpression au sein de la goutte. A l’équilibre, la pression dans la goutte, P_l, est donc supérieure à la pression extérieure, P.

Un raisonnement physique, qui ne sera pas développé ici, permet alors d’exprimer la différence de pression à l’interface : P_l - P en fonction des propriétés géométriques et de la tension superficielle g (de Gennes, 2002). C’est la loi de Laplace-Young :

                                                            Eq. 7

où R est le rayon de la goutte.

L’information principale de cette loi est que cette surpression est d’autant plus importante que le rayon de la goutte est petit. Ce résultat est généralisable pour une surface quelconque, par exemple à l’interface d’un ménisque, et conduit à des comportements remarquables comme l’ascension capillaire (cf. § Ascension capillaire) ou l’adhésion capillaire entre deux plaques.

Ascension capillaire - Loi de Jurin

Lorsqu’un tube est plongé dans un liquide (Figure 11), le liquide va, soit monter dans le tube (cas d’un liquide mouillant), soit se trouver à un niveau plus bas (cas d’un liquide non mouillant). Les forces capillaires sont directement responsables de ce phénomène, et la hauteur, h, à laquelle le liquide se stabilise, est le résultat d’un équilibre entre la force de pesanteur et les forces capillaires.

Pour établir la loi de Jurin, il suffit de dresser le bilan des forces en jeu. En appliquant la loi de Laplace-Young à l’interface entre le liquide et l’air (voir Eq. 7), il est possible de montrer que la différence de pression P_A à l’interface du ménisque est :

                                                                  Eq. 8

Or l’équilibre des pressions hydrostatiques à la base de la colonne (entre A et B – Figure 11) d’eau permet de connaître également P_A :

                                                       Eq. 9

Soit en remplaçant P_A par son expression, on obtient la loi de Jurin :

                                                                            Eq. 10

La loi de Jurin montre que la hauteur d’ascension est inversement proportionnelle au rayon, r, du tube utilisé et dépend des propriétés de « mouillage » du liquide sur la paroi. Dans le cas du mercure et d'un contenant en verre l’angle de contact q est supérieur à 90°, et la hauteur h est donc négative : le niveau du mercure dans le tube est inférieur au niveau à l’extérieur du tube. Ainsi l'on peut dire que le mercure est non mouillant sur du verre (Figure 3). A contrario, dans le cas de la sève sur du verre, l’angle de contact est inférieur à 90° et la hauteur h est positive. Le niveau dans le tube est donc plus haut que le niveau à l’extérieur (Figure 3). Dans ce cas le liquide est dit mouillant.

Toutefois il est important de garder à l’esprit que cette relation n’est valable que pour des tubes de faibles rayons i.e. des « capillaires ». En effet pour des tubes trop larges le ménisque ne se forme qu’à proximité des parois, la surface restante est alors plane et la différence de pression induite par la courbure du ménisque (Loi de Laplace-Young) n’est plus suffisante. L’ascension capillaire a donc lieu quand la largeur du tube est du même ordre de grandeur que les effets capillaires c’est-à-dire quand le rayon du tube est inférieur ou égale à la longueur capillaire ls (voir encart « Pour aller plus loin – Effet de la pesanteur »):

           soit                                             Eq. 11

Ainsi en utilisant la valeur de la tension superficielle de la sève brute qui varie entre 50 et 70 mN.m^-1 (Cf. Tableau 1), le rayon maximal de capillaire à partir de laquelle la loi de Jurin est importante varie entre 2.26 mm et 2.67 mm.